Tension in the wire connecting two blocks

In summary, two blocks with masses of 3.3 kg each are connected by wires CD and AB. The linear mass density of CD is 8X10^-3 and the linear mass density of AB is 10X10^-3. The speeds of transverse waves in AB and CD are v1 and v2 respectively. The tension in CD is 32N, and for AB it is equal to the weight of the upper block + weight of the second block + tension at the upper end. However, the weight of the rope and tension variations along the rope are unknown. If we neglect the tension and mass of the rope, the tension in AB would be 64N.
  • #1
harambe
50
10

Homework Statement


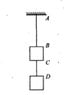
Two blocks each having masses of 3.3 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB.The linear mass density of the wire AB is 10X10^-3kgm^-1 and that of CD is 8X10^-3.The speeds of the transverse waves produced in AB and CD are respectively v1 and v2 .Then find v1 and v2

Homework Equations

The Attempt at a Solution



The tension in the wire CD is 32N but I am slightly confused for the Tension in AB.

For AB, The tension is going to be equal to the weight of the upper block +weight of the second block +weight of the rope+tension at the upper end but I don't know about the weight of the rope and also tension will vary across the rope so How should I proceed here
 

Attachments

  • 79bcf26d87a800c1a81b74bc46d39865.jpg
    79bcf26d87a800c1a81b74bc46d39865.jpg
    2.9 KB · Views: 488
Physics news on Phys.org
  • #2
CD supports the one weight below it and AB supports both weights below it. So what's the tension in AB?

On edit: Since the lengths of the wires are not given, you may ignore their masses for purposes of calculating the two tensions.
 
  • Like
Likes harambe
  • #3
You can assume that the weights of the wires are negligible compared to the weights of the blocks and you can also neglect the variation in tension between the bottom and top of each wire.
 
  • Like
Likes harambe
  • #4
That makes things easier then only the weight will act on the upper block
 
  • #5
If we neglect the tension and mass of rope then it would be 64N
 
  • #6
harambe said:
If we neglect the tension and mass of rope then it would be 64N
Yes, that's the tension in the upper wire. More correctly 64.7 N.
 
  • Like
Likes harambe

FAQ: Tension in the wire connecting two blocks

1. What causes tension in the wire connecting two blocks?

Tension in the wire is caused by the force applied to both ends of the wire in opposite directions, which creates a pulling or stretching effect. This tension is necessary to keep the blocks in place and prevent them from moving closer or farther away from each other.

2. How is tension measured in the wire connecting two blocks?

Tension is typically measured in units of force, such as Newtons, using a tension meter or by calculating the force required to stretch or compress the wire. The tension in the wire can also be determined by measuring the amount of deformation or elongation it experiences under the applied force.

3. What factors can affect the tension in the wire connecting two blocks?

The tension in the wire can be affected by the weight of the blocks, the angle at which the wire is pulled, the material and thickness of the wire, and the strength and direction of the applied force. Other factors such as friction and air resistance may also play a role in the tension of the wire.

4. Can the tension in the wire connecting two blocks be greater than the weight of the blocks?

Yes, the tension in the wire can be greater than the weight of the blocks if a greater force is applied to one or both ends of the wire. This is often seen in scenarios where the blocks are being lifted or pulled upwards, causing the tension to increase in order to support the weight of the blocks.

5. How does tension in the wire affect the stability of the blocks?

Tension in the wire plays a crucial role in maintaining the stability of the blocks. If the tension is too low, the blocks may move closer together or even collapse towards each other. On the other hand, if the tension is too high, the blocks may become unstable and start to move away from each other. Therefore, the tension must be carefully balanced to ensure the stability of the blocks.

Similar threads

Why is the tension force equal to friction force
Replies
9
Views
6K
What Determines Maximum Tension in a Cord Between Two Blocks on Inclined Planes?
Replies
25
Views
4K
Forces; Two blocks connected by a pulley with friction
Replies
1
Views
3K
What is the wavelength of a pulse on a hanging rope with changing tension?
Replies
15
Views
2K
Acceleration and Tension in a Two-Block System on an Inclined Plane
Replies
8
Views
2K
Finding Tension of a string tied to a wall
Replies
3
Views
6K
Find Acceleration & Tension in a System with Two Blocks and a Connecting Cord
Replies
6
Views
2K
Tension Rope and Blocks Problem
Replies
4
Views
6K
Tension in two ropes attached to a beam
Replies
8
Views
9K
Force, tension and blocks plx help
Replies
4
Views
947

Hot Threads

Recent Insights

Back
Top