Tension Problem (Two strings and an object)

[AY3]

1. A hemispherical sign in 1m diameter and of mass equal to 50kg is supported by two strings. Calculate the tension in the strings.

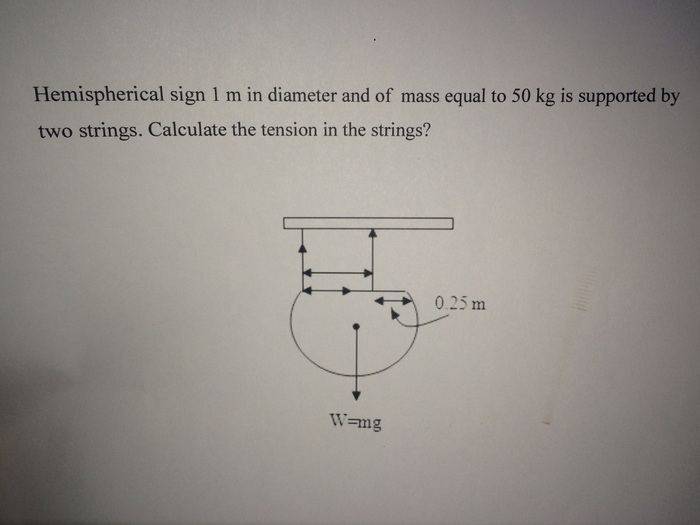
2. W = mg

3. I tried to solve it but the only thing I was able to do is knowing the distance between the two strings which is 0.75m, I'm new to physics.

 

[NascentOxygen]

Hi AY3. http://img96.imageshack.us/img96/5725/red5e5etimes5e5e45e5e25.gif

Identify a point about which you can take moments.

 

[AY3]

Do I create an X and Y axes and then do the sin and cos with an angle of 90 degrees?

 

[NascentOxygen]

Placing an x and a y-axis on the diagram would be a good first step.

It doesn't matter exactly where you locate them.

 

[AY3]

I solved it, the first step was creating an equation for the summition of force. I called the strings T2 and T2, the equation is T1+T2-W=0 because the object is in equilibrium. I have two unknowns in the equation. So the next step is determining the torque, assuming the point of rotation is T2.
Its equation was (T1*0.75)–(W*0.25)=0
In the end T1=166.67n and by substituting in the first equation T2=333.33n

 

[AY3]

I meant T1 and T2.