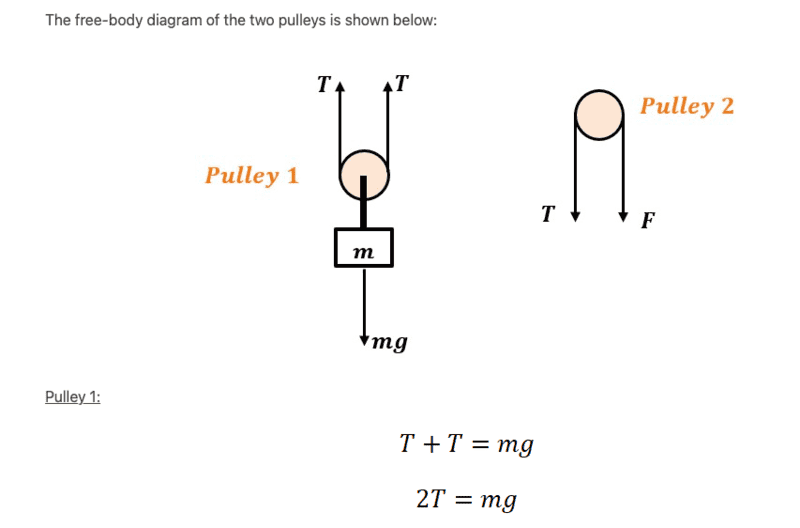Tension Question with One Mass and Two Pulleys

[singh101]

Homework Statement

Hello, with this question I understand how to setup and get the answer. However, I was confused by a few points which led me to getting the wrong answer.

Relevant Equations

F=ma

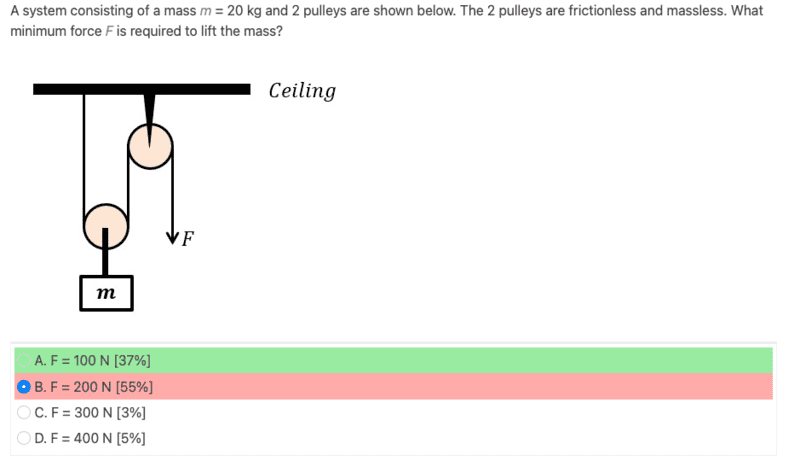
My question is how come the tension in pulley 2 is pointing downwards. I was under the impression that tension always points away from the mass.

 

[haruspex]

My question is how come the tension in pulley 2 is pointing downwards. I was under the impression that tension always points away from the mass.

Tension (likewise compression) is not a force; rather, it is pairs of equal and opposite forces all along a line through the body experiencing it (the rope, here).
At each end, the force a tension exerts on the adjacent body is away from that body. When drawing the FBD of the suspended mass, it points away from the mass; when drawing the FBD of the pulley above, it points away from the pulley.

 

[Delta2]

For a pulley the tension from the adjacent ropes always points away from the pulley, not towards the pulley.
Imagine you have a rope between two boxes, the tension at each of the points where the rope meets each of the boxes points away from the boxes.

 

[singh101]

So for a pulley the tension will always point away from the pulley.

 

[Delta2]

So for a pulley the tension will always point away from the pulley.

Yes, let me guess, your question is like, "How come at one end of the middle rope (where it meets pulley 1) the tension is upward and at the other end of the rope where it meets pulley 2 the tension is downwards? What exactly is happening inside the rope??" Is that your hidden question?

 

[singh101]

yes that was the thing that confused me because when setting up the question I put all the tension pointing upwards, however when I got the solution one of the tensions was point downwards.

 

[Delta2]

Well the answer lies on Newton's 3rd law and that the force from a rope to an adjacent body can only be attractive and not repulsive.

Why the force from a rope can be only attractive is a question that can be answered only by going into the realm of microscopic world which I don't want to do.

What Newton's 3rd law got to do here? Well imagine the infinitesimal portion $dx$ of the rope that is next to a pulley. According to Newton's 3rd the force from this dx of rope to the body (which can only be attractive as I said because we have a rope, newtons 3rd by default doesn't set requirement for attractive forces) lies on the line that connects the two bodies that is the piece of rope and the body.

 

[Lnewqban]

yes that was the thing that confused me because when setting up the question I put all the tension pointing upwards, however when I got the solution one of the tensions was point downwards.

Note that the shown FBD of pulley 2 is missing the force of the support (applied at the axis).
As that pulley is fixed to the ceiling, it can't accelerate or move vertically; therefore, a force must be acting in opposite direction respect to T and F, and with magnitude T+F.

If you consider that the only function of pulley 2 is to change the direction of the rope in such a way that the pulling effort is made more comfortable for a person standing on the ground, the tension still "points away from the mass".