Tensor algebra and the Projection Tensor

[Onamor]

Homework Statement

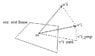
(firstly, Apologies for having to use a picture..)

If $$u^{i}$$ is the 4-velocity of a point on a manifold, then we use affine parameterisation $$g_{ij}u^{i}u^{j}=1$$.
The attached picture shows our rest frame, ie $$x^{0}=const$$ and a point ("us") on this surface. If our velocity is $$u^{i}$$ we want to describe the projection of another vector $$v^{i}$$ on to our velocity, $$u^{i}$$.

We define $$v^{i}=v^{i}_{para}+v^{i}_{perp}$$ the parallel and perpendicular components.

Homework Equations

(Mainly just algebra of tensors which I don't understand)

The Attempt at a Solution

This is a situation from my notes, so I have the answer but i don't understand the working...

$$v^{i}=u^{i}u_{j}v^{j}$$ (I already don't understand this line - why is this so? Isn't the contraction $$u_{j}v^{j}$$ on the RHS already a scalar product and hence a projection?)
gives $$v^{j}u_{j}=g_{jk}u^{k}v^{j}$$ (i think using $$g_{ij}u^{i}u^{j}=1$$?)
Now we write $$v^{i}_{para}=h^{i}_{j}v^{j}$$ where we define the projection $$h^{i}_{j}=\delta^{i}_{j}-u^{i}u_{j}$$.

Could someone run me through this working please? There is scarecly a line where I can see where it came from... And perhaps then, if i understand it, I could find $$v^{i}_{perp}$$.

Thank you very very much to any helpers.

 

[mark726]

Thank you for your post. Let me try to help you understand the working for this problem.

Firstly, let's start with the definition of the parallel and perpendicular components of a vector v^{i} with respect to a given 4-velocity u^{i}. This is given by v^{i}=v^{i}_{para}+v^{i}_{perp}, where v^{i}_{para} is the component of v^{i} that lies parallel to u^{i}, and v^{i}_{perp} is the component that is perpendicular to u^{i}.

Now, let's consider the expression v^{i}=u^{i}u_{j}v^{j}. This equation is known as the projection equation. It can be understood as follows: The 4-velocity u^{i} represents the direction in which we are projecting the vector v^{i}. The contraction u_{j}v^{j} on the right-hand side (RHS) of the equation represents the scalar projection of v^{i} onto u^{i}. This means that the RHS gives us the component of v^{i} that lies in the direction of u^{i}. Multiplying this by u^{i} gives us the vector v^{i}_{para} that is parallel to u^{i}.

Next, we use the fact that g_{ij}u^{i}u^{j}=1 to simplify the RHS of the projection equation. This is a normalization condition for the 4-velocity u^{i}. Multiplying both sides of the projection equation by g_{jk}u^{k} gives us v^{j}u_{j}=g_{jk}u^{k}v^{j}. This is just a rearrangement of terms.

Finally, we can write v^{i}_{para} in terms of the projection operator h^{i}_{j}. This operator is defined as h^{i}_{j}=\delta^{i}_{j}-u^{i}u_{j}, where \delta^{i}_{j} is the Kronecker delta symbol (which is equal to 1 if i=j and 0 otherwise). This operator essentially removes the component of u^{i} from v^{i}, leaving us with only the perpendicular component v^{i}_{perp}. Therefore, we can write v^{i}_{para}=h^{i}_{j}v^{j}, and hence, v^{