Engineering Tensor form of linear Hooke's law with E and v

[miraboreasu]

Homework Statement

Rewrite the linear Hooke's law with E and v

Relevant Equations

Linear Hooke's law

Actually, this is not homework, but I think I need help like homework. It was raised from the notice that there is no tensor form of linear Hooke's law in terms of Young's modulus E, and Poission's ratio, v. For example, if we use lame parameters, we have G, \lambda, like

The linear Hooke's law (vector-matrix form) is

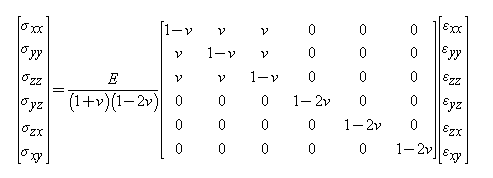
(https://physics.stackexchange.com/q...-materials-makes-stress-undefined-in-hookes-l)

I tried to just use the relationship like:
E=

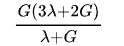
v =

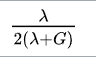
but, it ends up with an equation with 2 roots (the first eq for get G= f (E)), so I think I need help about write the notation form directly from the vector-matrix form of the linear Hooke's law

 

[Chestermiller]

Start with $$\sigma_{xx}=\frac{E}{(1+\nu)(1-2\nu)}[(1-\nu)\epsilon_{xx}+\nu\epsilon_{yy}+\nu\epsilon_{zz}]$$Rewrite this as :$$\sigma_{xx}=\frac{E}{(1+\nu)(1-2\nu)}[(1-2\nu)\epsilon_{xx}+\nu(\epsilon_{xx}+\epsilon_{yy}+\epsilon_{zz})]$$$$=\frac{E}{(1+\nu)}\epsilon _{xx}+\frac{E\nu}{(1+\nu)(1-2\nu)}(\epsilon_{xx}+\epsilon_{yy}+\epsilon_{zz})$$$$=2G\epsilon_{xx}+\lambda (\epsilon_{xx}+\epsilon_{yy}+\epsilon_{zz})$$

 

[miraboreasu]

Start with $$\sigma_{xx}=\frac{E}{(1+\nu)(1-2\nu)}[(1-\nu)\epsilon_{xx}+\nu\epsilon_{yy}+\nu\epsilon_{zz}]$$Rewrite this as :$$\sigma_{xx}=\frac{E}{(1+\nu)(1-2\nu)}[(1-2\nu)\epsilon_{xx}+\nu(\epsilon_{xx}+\epsilon_{yy}+\epsilon_{zz})]$$$$=\frac{E}{(1+\nu)}\epsilon _{xx}+\frac{E\nu}{(1+\nu)(1-2\nu)}(\epsilon_{xx}+\epsilon_{yy}+\epsilon_{zz})$$$$=2G\epsilon_{xx}+\lambda (\epsilon_{xx}+\epsilon_{yy}+\epsilon_{zz})$$

Thank you, but sorry I didn't get it, how can I rewrite the vector-matrix form into the form like 2.9. I mean use tensor product, I, to represent the following

 

[Chestermiller]

Thank you, but sorry I didn't get it, how can I rewrite the vector-matrix form into the form like 2.9. I mean use tensor product, I, to represent the following
View attachment 329468

Look at my equation again. It’s too easy. You have:$$G=\frac{E}{2(1+\nu)}$$and $$\lambda=\frac{E\nu}{(1+\nu)(1-2\nu)}$$