Terrell rotation is confusing!

[Physicsperson123]

Imagine in the distance you see a glowing spherical object hovering in the air.
Suppose light from point B on the surface of the sphere facing away from you can arrive at the camera simultaneously with light from A:

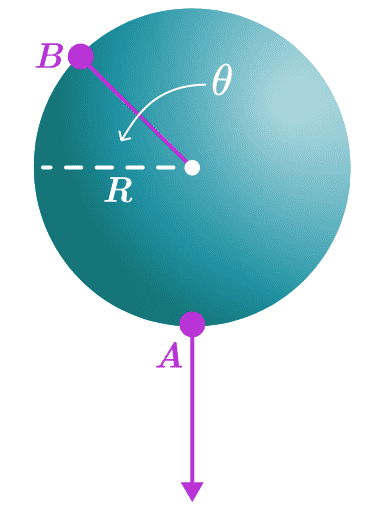
Since the object is moving at relativistic speeds, by the time light begins to propagate from A to reach your camera simultaneously with light from B, the object has already moved a certain distance.

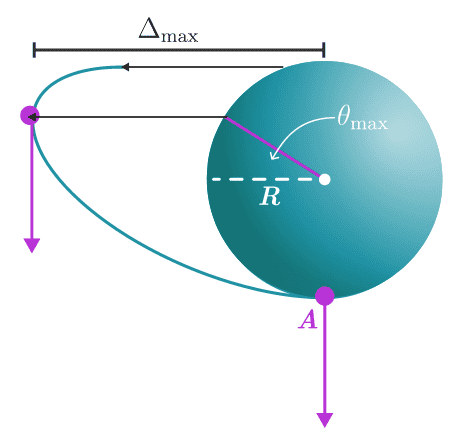
In this way one can see a rotation of the sphere by Θ_max.
What I don't understand about Terrell rotation is how light from point B would ever be able to reach an observer looking front on, because any straight path from point B would be blocked by the sphere.
I suspect that the light doesn't follow a straight path, and maybe this is where aberration of light comes in?
Any explanation would be greatly appreciated!

 

[Orodruin]

The path of the light only needs to be unblocked when the light arrives there.

 

[Nugatory]

how light from point B would ever be able to reach an observer looking front on, because any straight path from point B would be blocked by the sphere.

Take point B to right at the edge of the visible disk so it is just barely not blocked and it will make more sense.

I suspect that the light doesn't follow a straight path, and maybe this is where aberration of light comes in?

Light always travels in a straight line (gravitational effects introduce some subtleties in the definition "straight" but none of that is involved in this problem). Aberration affects the apparent angle at which the light reaches you but not the straight-line path between emission event and reception event.

 

[Physicsperson123]

The path of the light only needs to be unblocked when the light arrives there.

Sorry, I'm struggling to understand what you mean by "unblocked"

 

[A.T.]

What I don't understand about Terrell rotation is how light from point B would ever be able to reach an observer looking front on, because any straight path from point B would be blocked by the sphere.

The object moves slower than light, but it clears the light path faster than the light, because the intersection between the light path and the object moves faster than light. It's simpler to understand with a box:

From: https://www.spacetimetravel.org/bewegung/5

 

[Ibix]

What I don't understand about Terrell rotation is how light from point B would ever be able to reach an observer looking front on, because any straight path from point B would be blocked by the sphere.

One way to look at it is to think about light hypothetically emitted straight down from point B. In a small time $\delta t$ it would move down the page $c\delta t$. But in that same time the sphere has moved a small distance $v\delta t$ to the right. If you specify the latitude of B, you could work out how fast the sphere would have to be going so that it had moved far enough to be out of the way, in terms of $\delta t$ and $\theta$. Then you could take the limit as $\delta t\rightarrow 0$. Does the necessary speed converge to anything?

Another approach is just to derive relativistic aberration. In the rest frame of the sphere, write down the $x(t)$ and $y(t)$ positions of a pulse of light emitted by B, tangent to the surface of the sphere at B. This clearly does not intersect the surface of the sphere, right? Then use the Lorentz transforms to write down the $x'(t')$ and $y'(t')$ positions of the pulse of light. Clearly this cannot intersect the sphere because the light can't intersect the sphere in one frame but not another. Can you get $y'$ to be independent of $t'$? If so, it's travelling vertically without intersecting tge sphere.

 

[Vanadium 50]

First, do not use spheres.
Let me say that again. Do not use spheres.

Using something symmetric under rotation to understand rotations is a bad idea. Do not use spheres.

There are two effects. The object shrinks because of Lorentz contraction, and the object appears to stretch because of light travel time. To first order, these cancel. The residual 2nd order effect is the Terrell Rotation.

 

[A.T.]

The object moves slower than light, but it clears the light path faster than the light, because the intersection between the light path and the object moves faster than light. It's simpler to understand with a box:

From: https://www.spacetimetravel.org/bewegung/5

A consequence of this, is that while an omnidirectional light pulse propagates spherically in all inertial frames, the fraction of that sphere blocked by obstacles is frame dependent.

In the above example, the wavefront in the rest frame of the box is initially half of a sphere, while in the frame where the box moves, it is more than half of a sphere.

 

[Orodruin]

A consequence of this, is that while an omnidirectional light pulse propagates spherically in all inertial frames, the fraction of that sphere blocked by obstacles is frame dependent.

In the above example, the wavefront in the rest frame of the box is initially half of a sphere, while in the frame where the box moves, it is more than half of a sphere.

It should be noted that this is a direct consequence of the aberration of light.