- #36
- 3,486
- 257
Yes, that's right.Emspak said:Is the point here that even though fn approaches zero, and is less than some number no matter what you do with n (in this case the expression is always less than 1) that still does not imply uniform convergence?
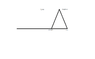
Here is an example: let ##f_n(x)## be the function whose graph looks like an isosceles triangle of height ##1## with one vertex at ##x = 1-1/n## and the other vertex at ##x=1##, and outside of ##[1-1/n, 1]##, the function is zero. This sequence satisfies ##|f_n(x)| \leq 1## for every ##n## and every ##x##. The sequence converges to ##0## for every ##x##, but not uniformly, because for every ##n## there is some ##x## (namely the midpoint of ##[1-1/n, 1]##) with ##f_n(x) = 1##.