- #1
DaniV
- 34
- 3
- Homework Statement
- Considering SU(N) gauge theory with nf massless quarks
I want to find the anomalous dimension to order of 1-loop of the massless quark field, that defined by: [ tex ]\gamma_q(g^{(R)})=\frac{1}{2Z_q}\mu\frac{\partial Z_q}{\partial \mu} [ /tex ]
when [ tex ]\mu [ /tex ] is energy scale, q is symbolize quark field, g is the strong coupling and $Z_q$ is the renormalization parameter such that: [ tex ]q^{(R)}=\frac{1}{\sqrt{Z_q}}q ,\bar q^{(R)}=\frac{1}{\sqrt{Z_q}}\bar q [ /tex ]
- Relevant Equations
- [ tex ]\gamma_q(g^{(R)})=\frac{1}{2Z_q}\mu\frac{\partial Z_q}{\partial \mu} [ /tex ]
[ tex ]q^{(R)}=\frac{1}{\sqrt{Z_q}}q ,\bar q^{(R)}=\frac{1}{\sqrt{Z_q}}\bar q [ /tex ]
I tried as first step to find [itex] Z_q [/itex] the renormalization parameter, to do so I did the same procedure to find the renormalization parameter of the gauge field of the gluon [itex]A^a_\mu[/itex] when [itex]a[/itex] is representation index [itex] a \in {1,2,...,N^2-1}[/itex] such that [tex] A^{a{(R)}}_{\mu}=\frac{1}{\sqrt{Z_A}}A^{a}_{\mu}[/tex]. the procedure is to find 1-loop correction to the 2 point function of the field A, as a result we find the 1-loop beta function of the coupling [itex] g [/itex]: [tex]\beta(g^{(R)})=-\frac{(g^{(R)})^2}{16\pi^2}\cdot \left(\frac{11N-2n_f}{3}\right)[/tex]
I try to find the 1-loop correction to the two point function of the quark field, to do so I have to take into account and calculate the following diagram (putting quark's field mass to zero):
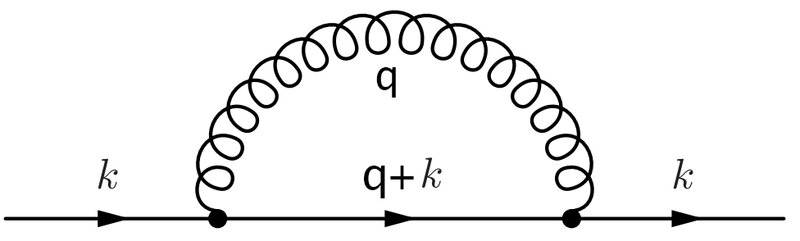
eventually I get the following effective action:
[tex]\Gamma=-\int d^dk \bar q^P(k) q^P(-k) \left[1-\frac{g^2}{32\pi^2} \cdot \left(\frac{1}{\epsilon}-\ln(k^2)+C \right) \right]k_\mu\gamma^\mu[/tex] when k is the momentum, and by dimensional regularization [itex] 2\epsilon=4-d[/itex], C is just a numerical value, and [itex] P\in 1,2,...,n_f [/itex] is the flavour index.
according to this effective action we define:
[tex] Z^{-1}_q=1-\frac{g^2}{32\pi^2} \cdot \left(\frac{1}{\epsilon}-\ln(\mu^2)+C \right) [/tex]
So the calculation of the anomalous dimension is depended on [itex] \beta(g^{(R)}) [/itex] but omitted because it have a coefficient with higher order value of g (taking all [itex] O(g^3) [/itex] to zero because it higher then 1-loop approximation).
the 1-loop anomalous dimension that I got is: [tex] \gamma_q(g^{(R)})=-\frac{(g^{(R)})^2}{32\pi^2} [/tex]
But I wonder if the answer have to be:
[tex] \gamma_q(g^{(R)})=-n_f\frac{(g^{(R)})^2}{32\pi^2} [/tex]
I claim that my previous answer is right because given a flavor P I can contract each flavor to itself and cannot contract with other flavors in order to build the loop correction we calculate earlier so we don`t need to multiply by $n_f$ the answer, moreover the definition of the anomalous dimension came from the Callan Symanzik equation for the n- correlator when the correlator for my opinion have to include n quarks with the same flavor (we can't contract different flavors) such that:
[tex] \left(n\gamma_q(g^{(R)})+\beta(g^{(R)})\frac{\partial}{\partial g^{(R)}}+\mu \frac{\partial}{\partial \mu}\right)G^{(R)}_{g^{R}(\mu)}(x_1,...,x_n)=0 [/tex]
when: [tex] G^{(R)}_{g^{R}(\mu)}(x_1,...,x_n)=\langle T[\bar q_P^{(R)}(x_1),q_P^{(R)}(x_2),..., \bar q_P^{(R)}(x_{n-1}),q_P^{(R)}(x_n)]\rangle=\mathcal N \int Dq D \bar q \bar D A q_P^{(R)}(x_1),q_P^{(R)}(x_2),..., \bar q_P^{(R)}(x_{n-1}),q_P^{(R)}(x_n)e^{iS[g^{(R)},A,q]} [/tex]
Am I right?
I try to find the 1-loop correction to the two point function of the quark field, to do so I have to take into account and calculate the following diagram (putting quark's field mass to zero):
eventually I get the following effective action:
[tex]\Gamma=-\int d^dk \bar q^P(k) q^P(-k) \left[1-\frac{g^2}{32\pi^2} \cdot \left(\frac{1}{\epsilon}-\ln(k^2)+C \right) \right]k_\mu\gamma^\mu[/tex] when k is the momentum, and by dimensional regularization [itex] 2\epsilon=4-d[/itex], C is just a numerical value, and [itex] P\in 1,2,...,n_f [/itex] is the flavour index.
according to this effective action we define:
[tex] Z^{-1}_q=1-\frac{g^2}{32\pi^2} \cdot \left(\frac{1}{\epsilon}-\ln(\mu^2)+C \right) [/tex]
So the calculation of the anomalous dimension is depended on [itex] \beta(g^{(R)}) [/itex] but omitted because it have a coefficient with higher order value of g (taking all [itex] O(g^3) [/itex] to zero because it higher then 1-loop approximation).
the 1-loop anomalous dimension that I got is: [tex] \gamma_q(g^{(R)})=-\frac{(g^{(R)})^2}{32\pi^2} [/tex]
But I wonder if the answer have to be:
[tex] \gamma_q(g^{(R)})=-n_f\frac{(g^{(R)})^2}{32\pi^2} [/tex]
I claim that my previous answer is right because given a flavor P I can contract each flavor to itself and cannot contract with other flavors in order to build the loop correction we calculate earlier so we don`t need to multiply by $n_f$ the answer, moreover the definition of the anomalous dimension came from the Callan Symanzik equation for the n- correlator when the correlator for my opinion have to include n quarks with the same flavor (we can't contract different flavors) such that:
[tex] \left(n\gamma_q(g^{(R)})+\beta(g^{(R)})\frac{\partial}{\partial g^{(R)}}+\mu \frac{\partial}{\partial \mu}\right)G^{(R)}_{g^{R}(\mu)}(x_1,...,x_n)=0 [/tex]
when: [tex] G^{(R)}_{g^{R}(\mu)}(x_1,...,x_n)=\langle T[\bar q_P^{(R)}(x_1),q_P^{(R)}(x_2),..., \bar q_P^{(R)}(x_{n-1}),q_P^{(R)}(x_n)]\rangle=\mathcal N \int Dq D \bar q \bar D A q_P^{(R)}(x_1),q_P^{(R)}(x_2),..., \bar q_P^{(R)}(x_{n-1}),q_P^{(R)}(x_n)e^{iS[g^{(R)},A,q]} [/tex]
Am I right?