The "agent" of energy flow for a gravitational slingshot?

[DoobleD]

Here is a gravitational slingshot figure from some homework exercise :

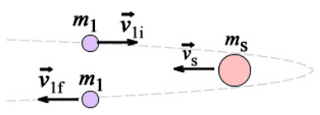
$m_1$ is a small mass, say, a space probe, and $m_s$ is Saturn. The direction of $m_1$'s velocity completely reverse direction due to Saturn's pull. $m_1$ come from very far away and end up very far away as well at the end.

Using conservation of momentum (and conservation of energy, if you're not resolving the problem from the center of mass frame of reference - approximated by Saturn's center), one can find out $v_{1f}$, the speed of $m_1$on its way back.

That speed ends up being $v_{1f} = v_{1i} + 2v_{s}$. $m_1$ has more kinetic energy after the "collision" than it had before. It stole some of Saturn's energy. Saturn's speed has decreased an infinitesimal amount (because it is so massive).

So energy has been transferred.

What annoys me is that I don't see any net work done (work done by gravity add up to 0 here right ?), or radiation, or heat, or so. What is the "agent" by which energy has been transferred ? By what mean does energy flow from Saturn to $m_1$ ?

Or is it just "conservation of momentum" and that's it ? Sounds quite different from usual cases where you can compute the work done by a force, or the quantity of heat transferred in a system, or the Poynting vector of an absorbed EM wave, and so on.

 

[jbriggs444]

So energy has been transferred.

Energy is not an invariant quantity. It varies with choice of reference frame. The amount of energy that is transferred (and in which direction) is also not an invariant quantity. It varies with choice of reference frame. It is, in effect, a mere book keeping entry rather than a real physical quantity.

You seem to be looking for a physical explanation for a book keeping entry. You will not find one.

 

[Dale]

What annoys me is that I don't see any net work done (work done by gravity add up to 0 here right ?), or radiation, or heat, or so. What is the "agent" by which energy has been transferred ?

Gravity. The work done by gravity on the slingshotted object is non-zero.

 

[DoobleD]

Thanks guys for answering.

Gravity. The work done by gravity on the slingshotted object is non-zero.

Ah? Hm, okay, let's try this :

If the net work done by gravity on the probe is non zero, that means that the work done on the probe during the approach (positive work) must be superior to the magnitude of the work done during the recession (negative work). The only way this can happen is if the distance traveled by the probe during recession is smaller than the distance traveled during the approach...

And this might make sense ! Let's draw a line mark where the probe starts. When the probe is back at the mark after it's journey, Saturn is closer than it was when the probe started the journey. Because Saturn has a velocity in the direction of the mark, during the whole journey. Thus, the distance between the probe and Saturn after the recession part is actually smaller than the distance between them before the approach. Thus, the work done during the recession part is lower.

Is that a correct understanding ?

 

[jbriggs444]

If the net work done by gravity on the probe is non zero, that means that the work done on the probe during the approach (positive work) must be superior to the magnitude of the work done during the recession (negative work). The only way this can happen is if the distance traveled by the probe during recession is smaller than the distance traveled during the approach...

Yes.

And this might make sense ! Let's draw a line mark where the probe starts. When the probe is back at the mark after it's journey, Saturn is closer than it was when the probe started the journey. Because Saturn has a velocity in the direction of the mark, during the whole journey. Thus, the distance between the probe and Saturn after the recession part is actually smaller than the distance between them before the approach. Thus, the work done during the recession part is lower.

I am not sure I understand this accounting scheme. You are measuring work done along a trajectory from a fixed point to the interaction with Saturn and back to the starting point. But the end of that trajectory is deeper in Saturn's gravitational well than the start. It's apples and oranges.

I prefer to model it more simply. Think of it as a baseball and a bat in an elastic collision. In a frame of reference in which a leftward-moving bat is moving toward a rightward moving ball the bat slows down and the rebounding ball has a net increase in speed. The leftward force of the bat place is applied over a non-negligible leftward displacement. Hence the increase in ball energy.

The interaction with Saturn (measured from some fixed distance away from Saturn and back to the same fixed distance away from Saturn) is a net leftward force applied over a net leftward displacement. Hence the net transfer of energy.

Switch to a different reference frame and the same interaction can be energy neutral or can drain energy (reverse slingshot).

 

[DoobleD]

The baseball and bat analogy is explicit. But in that case it's easier (for me) to see the actual work done, than it is for the slingshot case. Probably because in the baseball case, there is a an obvious force in only one direction applied for a distance. Initially for the slingshot case I thought the net work done by gravity was 0. That was the source of my confusion.

If the distance (relative to Saturn) on the return path is indeed shorter than on the approach path, then I have the answer I was looking for.

But the end of that trajectory is deeper in Saturn's gravitational well than the start. It's apples and oranges.

Well, if the relative distance between the probe and Saturn is shorter on the return path, then yes at the end the probe is a little deeper in Saturn's field than it was before approach, but why is this wrong ? That would be the reason why the work done on the return path is a little lower, because it misses a little work from the "deeper in field" position to the initial distance away from the field it had before the start. A very tiny amount of work missing.

 

[jbriggs444]

If the distance (relative to Saturn) on the return path is indeed shorter than on the approach path, then I have the answer I was looking for.

If you are measuring everything relative to Saturn then the slingshot will not provide any energy! The energy you gain by not moving as far is precisely the kinetic energy you get from being lower in the potential well. You have an explanation -- but you have nothing to explain in that reference frame.

 

[DoobleD]

If you are measuring everything relative to Saturn then the slingshot will not provide any energy!

If I approximate the whole system's center of mass as Saturn's center, and do the maths from there, the kinetic energy of the probe doesn't change indeed. But this is only a (very good) approximation right ?

The energy you gain by not moving as far is precisely the kinetic energy you get from being lower in the potential well. You have an explanation -- but you have nothing to explain in that reference frame.

Do you mean that the explanation that gravity does a non zero net work only holds outside of Saturn's reference frame ? Sorry if I misunderstand what you're saying.

EDIT : I'm not so sure anymore about the fact that the probe's kinetic energy doesn't change from Saturn's reference frame POV...Because the probe is lower in Saturn's field at the end, even from that POV.

 

[jbriggs444]

If I approximate the whole system's center of mass as Saturn's center, and do the maths from there, the kinetic energy of the probe doesn't change indeed. But this is only a (very good) approximation right ?

It is exact.

Do you mean that the explanation that gravity does a non zero net work only holds outside of Saturn's reference frame ? Sorry if I misunderstand what you're saying.

If you want to start and end at the same distance from Saturn (so that you are not just trading potential energy for kinetic energy) then the only way that Saturn's gravity can do net work is if Saturn is moving. That means that you have to adopt some frame of reference other than Saturn's rest frame.

EDIT : I'm not so sure anymore about the fact that the probe's kinetic energy doesn't change from Saturn's reference frame POV...Because the probe is lower in Saturn's field at the end, even from that POV.

But that is not what a gravitational slingshot is about. The point of a gravitational slingshot around Saturn is to make you move faster relative to the Sun, not faster relative to Saturn.

 

[Vanadium 50]

DoobnleD, you are making this way, way, way too hard. The physics of a slingshot is exactly the same as for an elastic collision. You are bouncing the probe off the planet. All using gravity does is make the process more gradual (so you have a probe recoil and not a bunch of probe parts),

 

[rcgldr]

On a side note, it works the other way as well. Have the satellite pass by in "front" of the planet and the satellite slows down. This is how objects can be transferred into orbits closer to the sun than the earth.

 

[just dani ok]

I think this video explains this situation pretty clearly. It even uses actual and quite current example to do it.

 

[DoobleD]

If you want to start and end at the same distance from Saturn (so that you are not just trading potential energy for kinetic energy).

Okay, I think I got confused before because I forgot that a gravitational slingshot is not about trading potential energy for kinetic energy, as you stated earlier actually. So, we want to start and end at same distance from Saturn, ok.

then the only way that Saturn's gravity can do net work is if Saturn is moving.

Hm, why is that ? Actually now that I consider same distance to Saturn before and after, I don't see how the net work done by Saturn can be different than 0 (no matter if Saturn moves or not, or the reference frame). :/ What am I missing again here ?

DoobnleD, you are making this way, way, way too hard. The physics of a slingshot is exactly the same as for an elastic collision.

In the case of a ball bouncing off a wall, for instance, I can see that one body applies a force on the other (and the other on the first), so that work is done between the two bodies, so that one gets more KE and the other lose a little KE.

In the gravitational slingshot case, while there is also an exchange of KE, I don't see where is the non 0 net work done (well I thought I understood it but no, see above). It's true that the two cases are similar. I just miss some understanding in the slingshot case.

Interestingly, in the ball/wall case, the small body loses KE and the big one gets KE, while in the slingshot case, the small body gains KE and the big one loses KE ! That's surprising.

As for the over-complicating things aspect, that's true I tend to do that and sometimes I confuse myself even more, sorry about that. :D

On a side note, it works the other way as well. Have the satellite pass by in "front" of the planet and the satellite slows down. This is how objects can be transferred into orbits closer to the sun than the earth.

Interesting !

I think this video explains this situation pretty clearly.

Yes I have come across this video some days ago, it's really nice.

 

[jbriggs444]

If you want to start and end at the same distance from Saturn (so that you are not just trading potential energy for kinetic energy) then the only way that Saturn's gravity can do net work is if Saturn is moving.

Hm, why is that ? Actually now that I consider same distance to Saturn before and after, I don't see how the net work done by Saturn can be different than 0 (no matter if Saturn moves or not). :/ What am I missing again here ?

There are a couple of ways to look at it.

If Saturn is stationary then its gravitational field is static. Gravity is a conservative force and has an associated potential. The only way you gain kinetic energy is by losing potential energy. And vice versa. We seem to be in agreement on that point. If Saturn is moving then its gravitational field (as seen from our chosen standard of rest) is changing over time. This opens up other possibilities.

But let us switch to a different viewpoint.

The easiest way is to use the analogy of a ball bouncing off a wall (as you proceed to do). The key point is that when the ball hits the wall, it is pushed. When the object slingshots around Saturn it is pulled. You seem to be focusing your attention on the long approach toward Saturn and the long departure from Saturn. But that is not where the important effect happens. The important part is when the object is very close to Saturn and is being pulled the hardest. That is where it gains its leftward (per the drawing) velocity.

If Saturn is at rest then the leftward velocity at which the object begins its departure from Saturn will be equal to the rightward velocity when it finishes its approach.

If Saturn is moving to the left then its leftward velocity relative to Saturn at departure will still be equal to its rightward velocity relative to Saturn at arrival. In our rightward-moving reference frame, its arrival velocity will be lower than this and its departure velocity will be higher than this. It will have gained energy.

One can account for this by noting that while it was whizzing by the moving Saturn at its point of closest approach, the object was moving leftward under a leftward force. That force was doing work on the object.

 

[Vanadium 50]

The kinematics of a gravitational slingshot are exactly the same as bouncing the probe off the planet. Don't look to find differences. You have an exchange of momentum and kinetic energy in both, and the amounts are exactly the same.

 

[DoobleD]

If Saturn is moving to the left then its leftward velocity relative to Saturn at departure will still be equal to its rightward velocity relative to Saturn at arrival.

Yes that I understand, and...

One can account for this by noting that while it was whizzing by the moving Saturn at its point of closest approach, the object was moving leftward under a leftward force. That force was doing work on the object.

THAT is what I was looking for !

If I get it correctly...To be sure : you say that during the rotation of the probe around the moving Saturn, after its velocity switched to the left, it is pulled to the left by Saturn's gravity a little more than it would have been if Saturn would have been at rest ? Which kind of makes sense, as Saturn is going away to the left, the pull has to be applied for a little more distance.

Is this a correct understanding of what you wrote ? Just as a double check.

The kinematics of a gravitational slingshot are exactly the same as bouncing the probe off the planet. Don't look to find differences. You have an exchange of momentum and kinetic energy in both, and the amounts are exactly the same.

Let's say the probe bounces off Saturn, instead of a gravity slingshot. Then, shouldn't the final KE of the probe be a little lower after collision ? As it is the case with a ball bouncing off a wall.

EDIT : I just realized I was comparing the slingshot to a ball/wall experiment where the wall doesn't move...That's wrong of course.

 

[A.T.]

Actually now that I consider same distance to Saturn before and after, I don't see how the net work done by Saturn can be different than 0 (no matter if Saturn moves or not, or the reference frame). :/ What am I missing again here ?

That the reference frame does matter, as already explained. Work is frame dependent.

Interestingly, in the ball/wall case, the small body loses KE

Not in the reference frame where the wall moves towards the ball. See this example, similar to sling shot in terms of energy:

 

[DoobleD]

That the reference frame does matter, as already explained. Work is frame dependent.

Yes, makes sense. In the center of mass reference frame approximated as Saturn's center, KE of the probe doesn't change and net work is 0. As explained earlier indeed.

Not in the reference frame where the wall moves towards the ball. See this example, similar to sling shot in terms of energy:

That's right, I just realized I was comparing two different cases. The wall has to move toward the ball to be in the same case as the gravitational slingshot configuration we are looking at. Thanks.

 

[A.T.]

In the center of mass reference frame approximated as Saturn's center,

For planning trajectories in the Solar system, the relevant reference frame is the center of mass of the Solar system (approximated as Sun's center).

 

[rcgldr]

On a side note, it works the other way as well. Have the satellite pass by in "front" of the planet and the satellite slows down. This is how objects can be transferred into orbits closer to the sun than the earth.

Interesting !

Note that even though an object is launched from earth, it can use the Earth to make better use of an rocket engine impulse to speed up or slow down the satellite. The impulse from a rocket engine, will produce the same change in velocity regardless of speed, so the effect is greatest if performed while passing by closely to a planet at high speed.

I also wonder about the case where a satellite is launched from the Earth at greater than escape velocity, make one elliptical orbit around the sun intercepting the Earth again for a gravity assist from the Earth without using gravity assist with any other planet.

Wiki articles:

http://en.wikipedia.org/wiki/Oberth_effect

http://en.wikipedia.org/wiki/MESSENGER