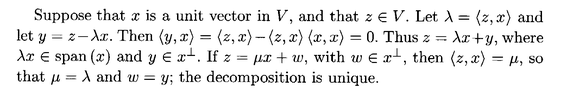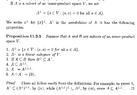The Annihilator of a Set ....Remarks by Garling After Proposition 11.3.5 ....

[Math Amateur]

I am reading D. J. H. Garling's book: "A Course in Mathematical Analysis: Volume II: Metric and Topological Spaces, Functions of a Vector Variable" ... ...

I am focused on Chapter 11: Metric Spaces and Normed Spaces ... ...

I need some help in order to understand the meaning and the point or reason for some remarks by Garling made after Proposition 11.3.5 ...

The remarks by Garling made after Proposition 11.3.5 ... read as follows:View attachment 8966I understand the "mechanics" of the equations/expressions in Garling's remarks but do not know the reason or the point of his remarks ... can someone please explain the reasons behind or the point of Garling's remarks ... further what does he mean by "decomposition" ... ... Help will be appreciated ...

Peter==========================================================================================

The above post refers to Proposition 11.3.5 ... so I am providing text of the same in order for readers to be able to understand the context of my question ...View attachment 8967Hope that helps ...

Peter

 

[Olinguito]

I understand the "mechanics" of the equations/expressions in Garling's remarks but do not know the reason or the point of his remarks ... can someone please explain the reasons behind or the point of Garling's remarks ... further what does he mean by "decomposition" ... ...

Garling is saying that any vector $z\in V$ can be written uniquely as $z=\lambda x+y$ where $\lambda$ is a scalar, $x$ is a unit vector and $y\in x^\bot$.

 

[soloenergy]

Hi Peter,

I haven't read the book you mentioned, but I can try to help you understand the remarks made by Garling in Proposition 11.3.5. From what I understand, Garling is discussing the concept of decomposition in metric spaces and normed spaces.

In mathematics, decomposition refers to breaking down a complex object or structure into simpler components. In the context of metric and normed spaces, it means finding a way to express a given space as a combination of simpler spaces. This can be useful in understanding the properties and structure of the space.

In Proposition 11.3.5, Garling is showing that every normed space can be decomposed into a direct sum of two subspaces, one of which is finite-dimensional and the other is infinite-dimensional. This result is important because it tells us that every normed space has a certain "structure" that can be broken down into simpler components.

The reason for Garling's remarks after the proposition may be to provide some intuition or explanation for why this decomposition is useful and what it tells us about the space. Without further context, it's hard to say exactly what he means by "mechanics" and "point" in this context, but I hope my explanation of decomposition has helped you understand the general idea.

If you have any specific questions about the equations or expressions in Garling's remarks, I suggest looking for more context in the book or asking for clarification from your instructor or classmates. Understanding mathematical concepts can be challenging, but with patience and practice, you'll get there. Good luck with your studies!