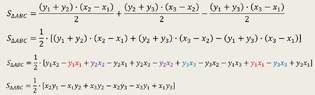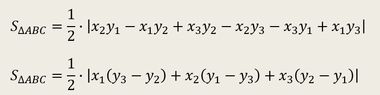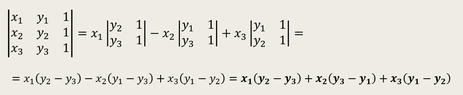MHB The area of a triangle and determinants

AI Thread Summary
The discussion centers on proving that the area of a triangle can be represented by a determinant formed by its three vertices. The original poster encounters issues with sign discrepancies in their proof, specifically regarding the orientation of the triangle. It is clarified that the determinant yields double the area for a counter-clockwise orientation, while a clockwise orientation results in a negative value. This indicates that the signs in the formulas must be adjusted based on the triangle's orientation. Understanding these orientation effects is crucial for aligning the two area representations.
Yankel
Messages
390
Reaction score
0
Dear all,

I was trying to prove that the area of a triangle is equal to the determinant consisting of the three points of the triangle. I got to the end, and something ain't working out. The signs are all wrong.

In the attached pictures I include my proof. Can you please tell me how can the two formulas be identical ? The first is the area coming from trapezoid subtraction , while the second is the determinant.

Thank you !

Clarification: when I say signs are opposite, I mean (y2-y3) vs. (y3-y2) , etc...

View attachment 7656

View attachment 7657

View attachment 7658

View attachment 7659
 

Attachments

  • 1.PNG
    1.PNG
    28.4 KB · Views: 110
  • 2.PNG
    2.PNG
    17.7 KB · Views: 120
  • 3.PNG
    3.PNG
    4.9 KB · Views: 106
  • 4.PNG
    4.PNG
    7.1 KB · Views: 119
Mathematics news on Phys.org
Hi Yankel,

The determinant gives double the area of a triangle that is oriented counter-clockwise.
In your case the triangle is oriented clockwise, meaning that we'll find the opposite.
 
Thread 'Video on imaginary numbers and some queries'

Thread 'Video on imaginary numbers and some queries'

Hi, I was watching the following video. I found some points confusing. Could you please help me to understand the gaps? Thanks, in advance! Question 1: Around 4:22, the video says the following. So for those mathematicians, negative numbers didn't exist. You could subtract, that is find the difference between two positive quantities, but you couldn't have a negative answer or negative coefficients. Mathematicians were so averse to negative numbers that there was no single quadratic...
View full post »
Thread 'Unit Circle Double Angle Derivations'

Thread 'Unit Circle Double Angle Derivations'

Here I made a terrible mistake of assuming this to be an equilateral triangle and set 2sinx=1 => x=pi/6. Although this did derive the double angle formulas it also led into a terrible mess trying to find all the combinations of sides. I must have been tired and just assumed 6x=180 and 2sinx=1. By that time, I was so mindset that I nearly scolded a person for even saying 90-x. I wonder if this is a case of biased observation that seeks to dis credit me like Jesus of Nazareth since in reality...
View full post »

Thread 'Fermat's Last Theorem'

Fermat's Last Theorem has long been one of the most famous mathematical problems, and is now one of the most famous theorems. It simply states that the equation $$ a^n+b^n=c^n $$ has no solutions with positive integers if ##n>2.## It was named after Pierre de Fermat (1607-1665). The problem itself stems from the book Arithmetica by Diophantus of Alexandria. It gained popularity because Fermat noted in his copy "Cubum autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et...
View full post »

Similar threads

MHB What is the area of triangle $STV$?
Replies
1
Views
1K
MHB Area of Triangle Shaded Region
Replies
5
Views
2K
MHB Prove Area of Equilateral Triangle
Replies
9
Views
2K
MHB Calculate Area of Triangle ABC
Replies
2
Views
5K
Comp Sci Computing the Length & Area of a 3D Triangle
Replies
1
Views
2K
MHB Equilateral triangle within a circumscribed circle
Replies
5
Views
3K
MHB Prove Equal Area Triangle & Parallelogram, $\angle ADC=90^{\circ}$
Replies
9
Views
3K
MHB How Can You Calculate the Area of a Polygon Using Coordinates?
Replies
3
Views
2K
Find the third coordinate of a vertex of an equilateral triangle
Replies
11
Views
10K
MHB Maximize Trapezoid Area with 3 Equal Sides | Leprofece Answer
Replies
1
Views
3K

Hot Threads

Recent Insights

Back
Top