- #1
Stephanus
- 1,316
- 104
Dear PF Forum,
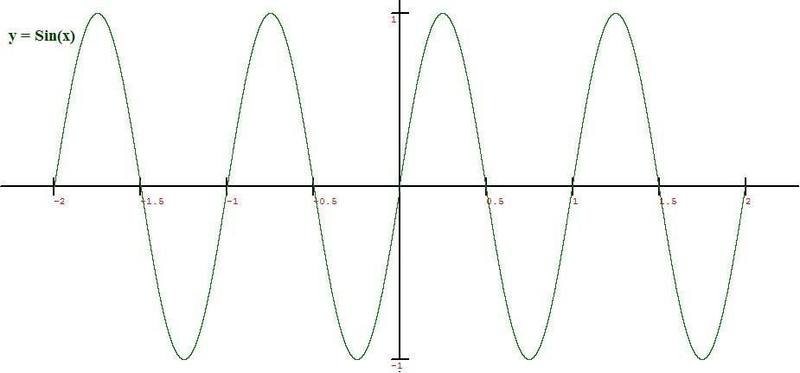
Finally I have written a simple software to plot Sin(X)
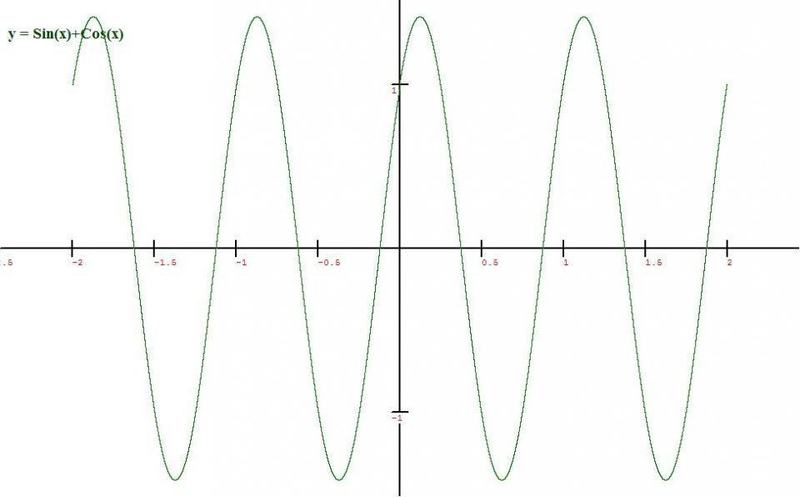
It can also draw y = sin(x) + cos(x). But I don't know how to use this function in real life.
This software is very simple.
All you need to do is altering this short function
Don't forget to alter this line also.
If you see the last line. LS.Add('y = Sin(x)/x');.
What if X is zero?
I cheat
Put catch exception in the code.
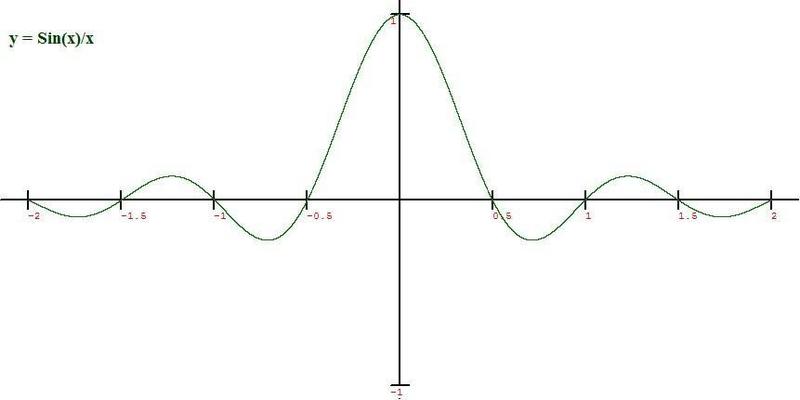
Funnily the computer still draw the curve as it is supposed to be.
And interesting enough. for sin(x)/x the biggest value is 1 for ##\lim_{h \to 0} \frac{\sin(h)}{h}##.
But how to proof that the biggest value for sin(x)/(x) is lim h -> 0?
The graph shows that, but we just can't say. "Well the graph shows that, so the biggest value for sin(x)/(x) is 1",
Anyone interested to proof it?
Finally I have written a simple software to plot Sin(X)
It can also draw y = sin(x) + cos(x). But I don't know how to use this function in real life.
This software is very simple.
All you need to do is altering this short function
Code:
case FDrawMode of
0: Result:=Sin(X)+Cos(X);
1: Result:=Sin(X);
2: Result:=Cos(X);
3: Result:=Sin(X)/X;
end;
Code:
LS:=edtDrawMode.Items;
LS.Clear;
LS.Add('y = Sin(x)+Cos(x)');
LS.Add('y = Sin(x)');
LS.Add('y = Cos(x)');
LS.Add('y = Sin(x)/x');What if X is zero?
I cheat
Put catch exception in the code.
Code:
try
Y:=ScaleY*Fc* CalcY(X+Sh); // case of sin(x)/x; if x = 0 then CalcY(X) will cause error.
YY:=Height1-Round(Y);
CV.Pixels[XX,YY]:=PlotColor;
except
// if error then don't draw anything
end;Funnily the computer still draw the curve as it is supposed to be.
And interesting enough. for sin(x)/x the biggest value is 1 for ##\lim_{h \to 0} \frac{\sin(h)}{h}##.
But how to proof that the biggest value for sin(x)/(x) is lim h -> 0?
The graph shows that, but we just can't say. "Well the graph shows that, so the biggest value for sin(x)/(x) is 1",
Anyone interested to proof it?