MarkFL
Gold Member
MHB
- 13,284
- 12
A problem that students in their first semester of elementary calculus commonly encounter involves taking a rectangular sheet of some material, and cutting squares from each corner so that when the resulting two pairs of flaps are folded up, an open box results. The students are asked to find the dimensions of the squares removed that will maximize the volume of the resulting box.
I thought it might be instructive to work the problem in general terms. Please refer to the following diagram:
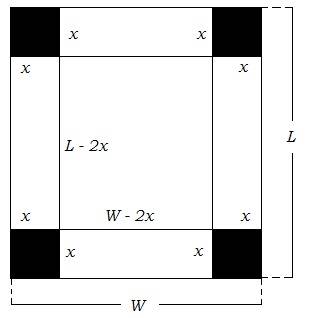
The width of the original sheet of material is labeled $W$ and the length if labeled $L$. The squares cut from the corners are shaded in black, and are $x$ units in length on a side.
As we can see, when the resulting flaps are folded up, the base of the box has area $A=(W-2x)(L-2x)$ and the height of the box is $x$, and so the volume of the box, as a function of $x$ is:
$$V(x)=x(W-2x)(L-2x)=4x^3-2(L+W)x^2+LWx$$
Differentiating with respect to $x$ and equating the result to zero, we find:
$$V'(x)=12x^2-4(L+W)x+LW=0$$
Now, if we observe that the derivative is parabolic, and opening upwards, then the smaller of the two roots must be at a local maximum, since the derivative will be positive to the left of this root and negative to the right. Hence, the smaller of the two roots, by the quadratic formula, is:
$$x=\frac{L+W-\sqrt{L^2-LW+W^2}}{6}$$
Another problem of this type involves taking a rectangular sheet and removing congruent rectangles from two adjacent corners, leaving a shape that can be folded into a closed box.
Please refer to the following diagram:
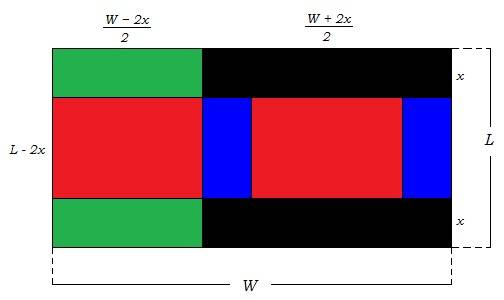
The removed rectangles are shaded in black, the base and top of the resulting box shaded in red, and the two pairs of opposing sides are shaded in green and in blue.
The area of the base is:
$$b=\frac{1}{2}(W-2x)(L-2x)$$
And since the height of the box is $x$, we find the volume of the box can be given by:
$$V(x)=bx=\frac{1}{2}(W-2x)(L-2x)x$$
If we recognize that this volume function is simply a constant times the volume function from the previous problem, then we know we will find the same critical value:
$$x=\frac{L+W-\sqrt{L^2-LW+W^2}}{6}$$
And so the width of the removed rectangles is:
$$w=\frac{W}{2}+x=\frac{L+4W-\sqrt{L^2-LW+W^2}}{6}$$
I thought it might be instructive to work the problem in general terms. Please refer to the following diagram:
The width of the original sheet of material is labeled $W$ and the length if labeled $L$. The squares cut from the corners are shaded in black, and are $x$ units in length on a side.
As we can see, when the resulting flaps are folded up, the base of the box has area $A=(W-2x)(L-2x)$ and the height of the box is $x$, and so the volume of the box, as a function of $x$ is:
$$V(x)=x(W-2x)(L-2x)=4x^3-2(L+W)x^2+LWx$$
Differentiating with respect to $x$ and equating the result to zero, we find:
$$V'(x)=12x^2-4(L+W)x+LW=0$$
Now, if we observe that the derivative is parabolic, and opening upwards, then the smaller of the two roots must be at a local maximum, since the derivative will be positive to the left of this root and negative to the right. Hence, the smaller of the two roots, by the quadratic formula, is:
$$x=\frac{L+W-\sqrt{L^2-LW+W^2}}{6}$$
Another problem of this type involves taking a rectangular sheet and removing congruent rectangles from two adjacent corners, leaving a shape that can be folded into a closed box.
Please refer to the following diagram:
The removed rectangles are shaded in black, the base and top of the resulting box shaded in red, and the two pairs of opposing sides are shaded in green and in blue.
The area of the base is:
$$b=\frac{1}{2}(W-2x)(L-2x)$$
And since the height of the box is $x$, we find the volume of the box can be given by:
$$V(x)=bx=\frac{1}{2}(W-2x)(L-2x)x$$
If we recognize that this volume function is simply a constant times the volume function from the previous problem, then we know we will find the same critical value:
$$x=\frac{L+W-\sqrt{L^2-LW+W^2}}{6}$$
And so the width of the removed rectangles is:
$$w=\frac{W}{2}+x=\frac{L+4W-\sqrt{L^2-LW+W^2}}{6}$$
Attachments
Last edited by a moderator: