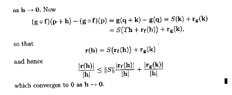Math Amateur
Gold Member
MHB
- 3,920
- 48
I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...
I am currently reading Chapter 8: Differentiable Maps and am specifically focused on Section 8.2 Differentials ... ...
I need some further help in order to fully understand the proof of Theorem 8.15 ...
Theorem 8.15 and its proof read as follows:
View attachment 9416
View attachment 9417In the above proof by Browder we read the following:" ... ... Now
$$(g \circ f) (p + h) - (g \circ h) (p) = g(q + k) - g(q)$$ ... ... "
Can someone please show how/why $$(g \circ f) (p + h) - (g \circ h) (p) = g(q + k) - g(q)$$ ... ...
Help will be appreciated ...
Peter
I am currently reading Chapter 8: Differentiable Maps and am specifically focused on Section 8.2 Differentials ... ...
I need some further help in order to fully understand the proof of Theorem 8.15 ...
Theorem 8.15 and its proof read as follows:
View attachment 9416
View attachment 9417In the above proof by Browder we read the following:" ... ... Now
$$(g \circ f) (p + h) - (g \circ h) (p) = g(q + k) - g(q)$$ ... ... "
Can someone please show how/why $$(g \circ f) (p + h) - (g \circ h) (p) = g(q + k) - g(q)$$ ... ...
Help will be appreciated ...
Peter