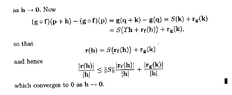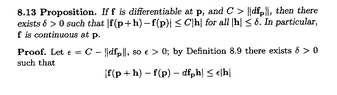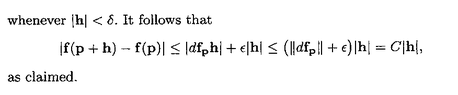The Chain Rule in n Dimensions .... Browder Theorem 8.15

[Math Amateur]

I am reading Andrew Browder's book: "Mathematical Analysis: An Introduction" ... ...

I am currently reading Chapter 8: Differentiable Maps and am specifically focused on Section 8.2 Differentials ... ...

I need some help in order to fully understand the proof of Theorem 8.15 ...

Theorem 8.15 and its proof read as follows:

View attachment 9412
View attachment 9413

In the above proof by Browder we read the following:" ... ... Then \(\displaystyle |k| \leq C |h|\) for \(\displaystyle |h|\) sufficiently small, if \(\displaystyle C \gt \| T \|\), by Proposition 8.13; it follows that

\(\displaystyle \frac{ r_g ( k(h) ) }{ |h| } \to 0\) as \(\displaystyle h \to 0\). ... ... "
My question is as follows:Can someone demonstrate formally and rigorously how/why \(\displaystyle \frac{ r_g ( k(h) ) }{ |h| } \to 0\) as \(\displaystyle h \to 0\). ... ...
Help will be much appreciated ...Peter==============================================================================The above post mentions Proposition 8.13 ... Proposition 8.13 reads as follows:
View attachment 9414
View attachment 9415
Hope that helps ...

Peter

 

[jvicens]

Dear Peter,

Thank you for reaching out for help with the proof of Theorem 8.15 in Andrew Browder's book. I will try my best to explain the formal and rigorous reasoning behind the statement \frac{ r_g ( k(h) ) }{ |h| } \to 0 as h \to 0.

First, let's recall the definitions of the terms involved in the statement. The function k(h) represents the differential of the map g at the point a, denoted by dg_a. This means that k(h) is the linear approximation of g at the point a, which can be written as:

g(a+h) = g(a) + k(h) + r_g(h)

where r_g(h) is the remainder term, which satisfies the following property:

\lim_{h \to 0} \frac{r_g(h)}{|h|} = 0

This means that as h approaches 0, the remainder term becomes smaller and smaller compared to the size of h.

Now, let's look at the expression \frac{ r_g ( k(h) ) }{ |h| }. This can be rewritten as:

\frac{ r_g ( k(h) ) }{ |h| } = \frac{r_g(h)}{|h|} \cdot \frac{|k(h)|}{|h|}

Since we know that \lim_{h \to 0} \frac{r_g(h)}{|h|} = 0, we just need to show that \frac{|k(h)|}{|h|} remains bounded as h approaches 0. This is where Proposition 8.13 comes in. Proposition 8.13 states that if the differential of a map is bounded by some constant C, then the map itself is Lipschitz continuous with Lipschitz constant C.

In our case, we know that |k(h)| \leq C |h| for |h| sufficiently small, if C \gt \| T \|, which means that the differential k(h) is bounded by some constant C. Therefore, by Proposition 8.13, we can conclude that the map g is Lipschitz continuous with Lipschitz constant C. This means that \frac{|k(h)|}{|h|} is also bounded by C.

Putting everything together, we have:

\frac{ r_g ( k(h) ) }{ |h|