- #1
PainterGuy
- 940
- 70
Moved from a technical forum and thus no template.
Hi!
I was trying to understand circular motion and came across two problems. I would really appreciate if you could help me with those.
Question 1:
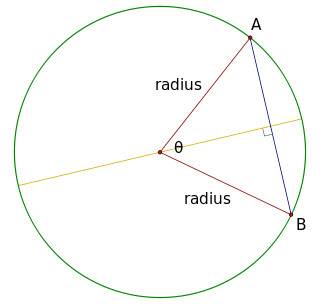
In the picture below let's assume that the angle θ is 1 radian, i.e. 57.3°, radius is 1 m. It would mean that the length of arc AB is also 1 m. The length of chord AB is 2*r*sin(θ/2) = 2*1*sin(57.3°/2) = 1 m
How could be the length of chord and arc equal? It doesn't make any sense to me. The length of arc should be more than that of the chord. Where am I having it wrong?
Question 2:
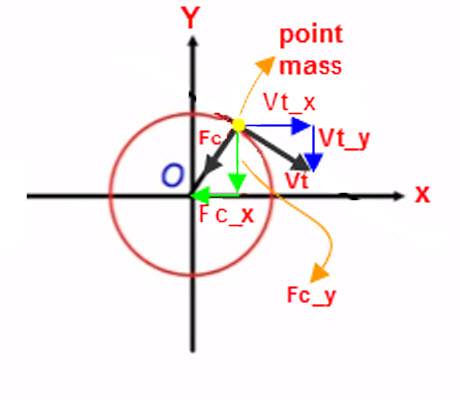
In the picture, it might be that I'm incorrectly resolving the vectors into components. A point mass is following a circular motion in clockwise direction. The centripetal force vector Fc is resolved into Fc_x and Fc_y components, and the tangential velocity vector Vt is resolved into Vt_x and Vt_y. The components Fc_y and Vt_y are in the same direction. But weren't force vector and velocity vector supposed to not have any components parallel to each other? Where am I going wrong? Please help me.
I was trying to understand circular motion and came across two problems. I would really appreciate if you could help me with those.
Question 1:
In the picture below let's assume that the angle θ is 1 radian, i.e. 57.3°, radius is 1 m. It would mean that the length of arc AB is also 1 m. The length of chord AB is 2*r*sin(θ/2) = 2*1*sin(57.3°/2) = 1 m
How could be the length of chord and arc equal? It doesn't make any sense to me. The length of arc should be more than that of the chord. Where am I having it wrong?
Question 2:
In the picture, it might be that I'm incorrectly resolving the vectors into components. A point mass is following a circular motion in clockwise direction. The centripetal force vector Fc is resolved into Fc_x and Fc_y components, and the tangential velocity vector Vt is resolved into Vt_x and Vt_y. The components Fc_y and Vt_y are in the same direction. But weren't force vector and velocity vector supposed to not have any components parallel to each other? Where am I going wrong? Please help me.



