- #1
ThangMMM
- 2
- 0
I'm studying about piezoelectric material. The electro - mechanical property of this material can be described by the following constitutive equation:
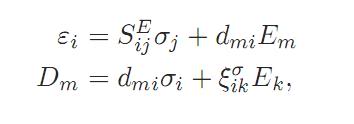
Sij is the compliance matrix, and dmi is the piezoelectric constant for the materials
The matrix form of the equation:
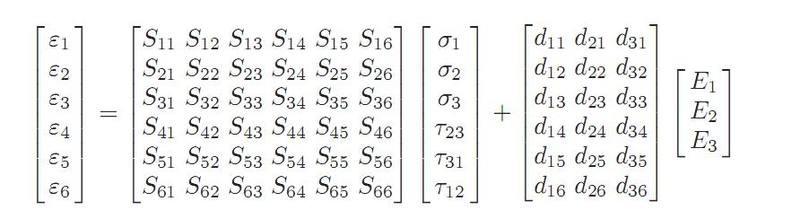
Applying this equation for PZT (lead zirconate titanate) materials with tetragonal perovskite structure, some of these above Sij and dmi can be equal, or zero. The equation becomes:
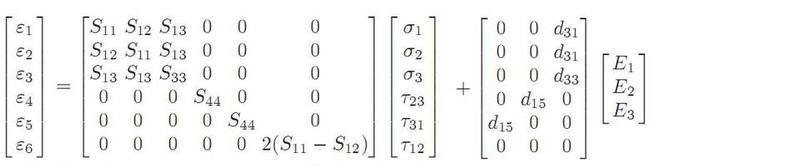
I'm concerning about why S31 = S32 = S13 = S23 and S66 = 2(S11 - S12) ??
When I'm reading some documents about PZT, they usually classify PZT into PZT-4, PZT-5, etc (like this: http://www.efunda.com/Materials/piezo/material_data/matdata_index.cfm ). What does these number after it means ?
thank you very much\..
Sij is the compliance matrix, and dmi is the piezoelectric constant for the materials
The matrix form of the equation:
Applying this equation for PZT (lead zirconate titanate) materials with tetragonal perovskite structure, some of these above Sij and dmi can be equal, or zero. The equation becomes:
I'm concerning about why S31 = S32 = S13 = S23 and S66 = 2(S11 - S12) ??
When I'm reading some documents about PZT, they usually classify PZT into PZT-4, PZT-5, etc (like this: http://www.efunda.com/Materials/piezo/material_data/matdata_index.cfm ). What does these number after it means ?
thank you very much\..