PainterGuy
- 938
- 73
Hi,
The quote below has been taken from this article, https://math.ucr.edu/home/baez/einstein/node2.html, which I came across.
The quote doesn't make any sense to me, especially the part in boldface. Could you please help me with it?
The quote below has been taken from this article, https://math.ucr.edu/home/baez/einstein/node2.html, which I came across.
Similarly, in general relativity gravity is not really a `force', but just a manifestation of the curvature of spacetime. Note: not the curvature of space, but of spacetime. The distinction is crucial. If you toss a ball, it follows a parabolic path. This is far from being a geodesic in space: space is curved by the Earth's gravitational field, but it is certainly not so curved as all that! The point is that while the ball moves a short distance in space, it moves an enormous distance in time, since one second equals about 300,000 kilometers in units where. This allows a slight amount of spacetime curvature to have a noticeable effect.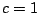
The quote doesn't make any sense to me, especially the part in boldface. Could you please help me with it?