MarkFL
Gold Member
MHB
- 13,284
- 12
Resident number theorist and global moderator at MMF (Charles R Greathouse IV) has graciously given me permission to reproduce an image he created to demonstrate the different classes of numbers:
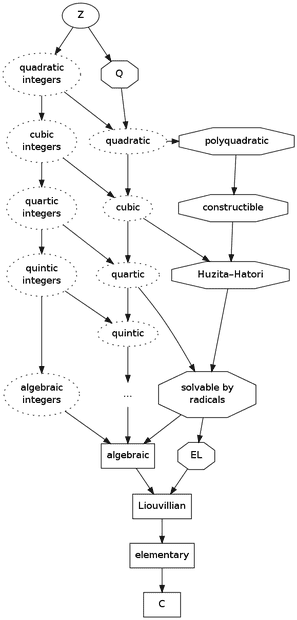
Rings are depicted in a ring, fields in an octagon, and algebraically closed fields in a rectangle. Objects in dashed rings are just sets (usually not even closed under addition!).
Key:
$\mathbb{Z}$: the ring of integers $\{..., -2, -1, 0, 1, ...\}$.
$\mathbb{Q}$: the field of rational numbers.
quadratic (etc.) integers: the root of a monic quadratic (etc.) polynomial in the integers.
quadratic (etc.) numbers: the root of a quadratic (etc.) polynomial in the integers.
polyquadratic numbers: numbers of the form $\sqrt{a_1}+\sqrt{a_2}+\cdots+\sqrt{a_k}$ with $a_i$ rational; see Conway, Radin, & Sadun.
constructible numbers: numbers which can be formed from field operations plus extraction of square roots, for example $\sqrt{4 + \sqrt{7}}$.
Huzita-Hatori numbers: numbers which can be formed from the field operations plus extraction of square and cube roots.
algebraic integers: the root of a monic polynomial in the integers.
algebraic numbers: the root of a polynomial in the integers.
solvable by radicals: numbers which can be formed from the field operations plus extraction of $n$-th roots.
$EL$ numbers: the smallest subfield of $\mathbb{C}$ closed under $\exp$ and $\log$, allowing explicit roots like $\exp\left(\dfrac{\log(x)}{5} \right)$; Chow writes $E$ for this.
Liouvilian numbers: algebraic closure of $EL$, allowing finding arbitrary roots in addition to $\exp$ and $\log$; sometimes written $L$.
elementary numbers: extension of Liouvilian numbers allowing implicit $\exp$ and $\log$
periods: multidimensional integrals of rational functions; see Kontsevich & Zagier.
exponential periods: the (algebraic?) closure of periods and exponentials of periods; see Kontsevich & Zagier.
$\mathbb{C}$: the complex numbers.
References:
Timothy Y. Chow, http://math.mit.edu/~tchow/closedform.pdf, The American Mathematical Monthly 106:5 (1999), pp. 440-448.
John H. Conway, Charles Radin, and Lorenzo Sadun, On Angles Whose Squared Trigonometric Functions are Rational, Discrete Computational Geometry 22 (1999), pp. 321-332.
Maxim Kontsevich and Don Zagier, Periods, in "Mathematics Unlimited, Year 2001 and Beyond", Eds. B.Engquist and W.Scmidt, Springer, 2001.
Rings are depicted in a ring, fields in an octagon, and algebraically closed fields in a rectangle. Objects in dashed rings are just sets (usually not even closed under addition!).
Key:
$\mathbb{Z}$: the ring of integers $\{..., -2, -1, 0, 1, ...\}$.
$\mathbb{Q}$: the field of rational numbers.
quadratic (etc.) integers: the root of a monic quadratic (etc.) polynomial in the integers.
quadratic (etc.) numbers: the root of a quadratic (etc.) polynomial in the integers.
polyquadratic numbers: numbers of the form $\sqrt{a_1}+\sqrt{a_2}+\cdots+\sqrt{a_k}$ with $a_i$ rational; see Conway, Radin, & Sadun.
constructible numbers: numbers which can be formed from field operations plus extraction of square roots, for example $\sqrt{4 + \sqrt{7}}$.
Huzita-Hatori numbers: numbers which can be formed from the field operations plus extraction of square and cube roots.
algebraic integers: the root of a monic polynomial in the integers.
algebraic numbers: the root of a polynomial in the integers.
solvable by radicals: numbers which can be formed from the field operations plus extraction of $n$-th roots.
$EL$ numbers: the smallest subfield of $\mathbb{C}$ closed under $\exp$ and $\log$, allowing explicit roots like $\exp\left(\dfrac{\log(x)}{5} \right)$; Chow writes $E$ for this.
Liouvilian numbers: algebraic closure of $EL$, allowing finding arbitrary roots in addition to $\exp$ and $\log$; sometimes written $L$.
elementary numbers: extension of Liouvilian numbers allowing implicit $\exp$ and $\log$
periods: multidimensional integrals of rational functions; see Kontsevich & Zagier.
exponential periods: the (algebraic?) closure of periods and exponentials of periods; see Kontsevich & Zagier.
$\mathbb{C}$: the complex numbers.
References:
Timothy Y. Chow, http://math.mit.edu/~tchow/closedform.pdf, The American Mathematical Monthly 106:5 (1999), pp. 440-448.
John H. Conway, Charles Radin, and Lorenzo Sadun, On Angles Whose Squared Trigonometric Functions are Rational, Discrete Computational Geometry 22 (1999), pp. 321-332.
Maxim Kontsevich and Don Zagier, Periods, in "Mathematics Unlimited, Year 2001 and Beyond", Eds. B.Engquist and W.Scmidt, Springer, 2001.
Attachments
Last edited by a moderator: