Petrus
- 702
- 0
Hello MHB,
I wanted to 'challange' myself with solve a problem with midpoint and rule and the double integral f over the rectangle R.
This is a problem from midpoint.
"Use the Midpoint Rule m=n=2 to estimate the value of the integrab $$\int\int_r(x-3y^2)dA$$, where $$R= {(x,y)| 0\leq x \leq 2, 1 \leq y \leq 2}.$$
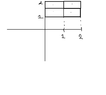
Let's start with mid point. I Always start with draw itView attachment 738
and the center of those four subrectangles is $$x_1=\frac{1}{2}$$, $$x_2= \frac{3}{2}$$, $$y_1=\frac{5}{4}$$ and $$y_2=\frac{7}{4}$$ and the area of the sub rectangle is $$A= \frac{1}{2}$$ to make it more clear we got $$\frac{1}{2}(f(\frac{1}{2},\frac{5}{4})+f(\frac{1}{2},\frac{7}{4})+f(\frac{3}{2},\frac{5}{4})+f(\frac{3}{2},\frac{7}{4})=-11.875$$
this question is aproxomite same as
$$\int_1^2\int_0^2 x-3y^2 dxdy$$ and that will give result $$-13$$
Now for the most chalange one that I can't solve
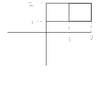
I can only solve it with $$m=2$$$$n=1$$(we got two subs in x and 1 in y. cause then we get I start as usually draw it :) View attachment 739 then we got the area of sub square $$A=1$$ so we got these point $$f(1,2)+f(2,2)$$
and we get result $$-9$$. Now afterwards I type I notice we can't use the rule right? $$x-3y^2=z$$ and for any of our point we will get $$z<0$$ and then we can't use defination. but are my two above correct?Regards,
I wanted to 'challange' myself with solve a problem with midpoint and rule and the double integral f over the rectangle R.
This is a problem from midpoint.
"Use the Midpoint Rule m=n=2 to estimate the value of the integrab $$\int\int_r(x-3y^2)dA$$, where $$R= {(x,y)| 0\leq x \leq 2, 1 \leq y \leq 2}.$$
Let's start with mid point. I Always start with draw itView attachment 738
and the center of those four subrectangles is $$x_1=\frac{1}{2}$$, $$x_2= \frac{3}{2}$$, $$y_1=\frac{5}{4}$$ and $$y_2=\frac{7}{4}$$ and the area of the sub rectangle is $$A= \frac{1}{2}$$ to make it more clear we got $$\frac{1}{2}(f(\frac{1}{2},\frac{5}{4})+f(\frac{1}{2},\frac{7}{4})+f(\frac{3}{2},\frac{5}{4})+f(\frac{3}{2},\frac{7}{4})=-11.875$$
this question is aproxomite same as
$$\int_1^2\int_0^2 x-3y^2 dxdy$$ and that will give result $$-13$$
Now for the most chalange one that I can't solve
I can only solve it with $$m=2$$$$n=1$$(we got two subs in x and 1 in y. cause then we get I start as usually draw it :) View attachment 739 then we got the area of sub square $$A=1$$ so we got these point $$f(1,2)+f(2,2)$$
and we get result $$-9$$. Now afterwards I type I notice we can't use the rule right? $$x-3y^2=z$$ and for any of our point we will get $$z<0$$ and then we can't use defination. but are my two above correct?Regards,