The efficiency of a heat engine

[gregorspv]

Homework Statement

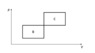
An ideal monoatomic gas (ϰ=5/3) is repeating a thermodynamic cycle B, which is made out of two isobaric and two isochoric parts. The same gas is repeating a similar cycle C. Both cycles have the same ΔP and ΔV. Express cycle B's efficiency in terms of the efficiency of cycle A.

Relevant Equations

Q=mcΔT
η=A/Qin
dA=PdV

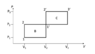
The first picture was provided along the problem statement. The second has my annotations.

I initially began by calculating the ratio of efficiencies, since the work done is obviously the same and cancels out, but after failing and having seen the form of the solution I saw that that cannot work. Therefore I first derived the expression for the efficiency of cycle B: $$\eta_B=\frac{A}{Q_{in,B}}=\frac{\Delta P\Delta V}{mc_V(T_2-T_1)+mc_P(T_{1'}-T_2)}=\frac{\Delta P\Delta V}{mc_V(T_1\frac{P_2}{P_1}-T_1)+mc_P(T_2\frac{V_2}{V_1}-T_2)}=\frac{\Delta P\Delta V}{mc_VT_1(\frac{P_2}{P_1}-1)+mc_PT_1\frac{P_2}{P_1}(\frac{V_2}{V_1}-1)}=\frac{\Delta P\Delta V}{mT_1}\frac{1}{c_V(\frac{P_2}{P_1}-1)+c_P\frac{P_2}{P_1}(\frac{V_2}{V_1}-1)}$$
and similarly
$$\eta_C=\frac{A}{Q_{in,C}}=\frac{\Delta P\Delta V}{mc_V(T_{2'}-T_{1'})+mc_P(T_{3}-T_{2'})}=\frac{\Delta P\Delta V}{mc_VT_1\frac{P_2}{P_1}\frac{V_2}{V_1}(\frac{P_3}{P_2}-1)+mc_P\frac{P_3}{P_1}\frac{V_2}{V_1}(\frac{V_3}{V_2}-1)}=\frac{1}{mT_1}\frac{1}{c_V\frac{V_2}{V_1}\frac{1}{P_1\Delta V}+c_P\frac{P_2}{P_1}\frac{1}{V_1\Delta P}+c_P\frac{1}{P_1V_1}}$$

I then substituted $\eta_B$ into $\eta_C$ to obtain: $$\eta_C=\eta_B(\frac{1}{P_1\Delta V}+\frac{\kappa}{V_1 \Delta P}+\frac{\kappa}{P_1V_1})\frac{1}{\frac{V_2}{V_1}\frac{1}{P_1\Delta V}+\frac{P_2}{P_1}\frac{\kappa}{V_1 \Delta P}+\frac{\kappa}{P_1V_1}}=\eta_B\frac{1}{1+\frac{\Delta V\Delta P+\kappa\Delta P\Delta V}{V_1\Delta P + \kappa P_1\Delta V + \kappa \Delta V\Delta P}}$$

The solution I was given is: $$\eta_C=\eta_B\frac{1}{1+4\eta_B}$$ but this seems incompatible with my derivation. I should suppose there is a much simpler way of approaching this problem?

 

[Andrew Mason]

First of all: what is cycle A?

One has to determine the heat flow in each segment in which there is heat flow into the system. To do that you need to determine the temperatures at the cornerns. Use PV=nRT.

To find the heat flow at constant volume for the isochoric segment use Q = nC_vΔT; For the isobaric part use Q = nC_pvΔT

AM

 

[gregorspv]

Oh, I must have made a typo; the actual problem is to express the efficiency of C in terms of B. Not sure why they're labelled that way though.

I believe the heat flows $Q_{in}$ were determined correctly? I expressed the temperatures in terms of pressure, volume and $T_1$ via Charles's ($\frac{V}{T}=const.$) and Gay-Lussac's laws ($\frac{P}{T}=const.$). Then I substituted those expressions into the two equations containing the specific heat term: this can be seen in the efficiencies' denominators. I did omit a few steps in my post due to tiresome LaTeX. Do you think I have made an arithmetic mistake?

 

[Chestermiller]

Try setting the problem up a little differently. Call the pressure and volume at point 1' P and V. Then for process B, the coordinates of the corners would be $(P-\Delta P, V-\Delta V)$, $(P,V-\Delta V)$, $(P, V)$, and $(P-\Delta P, V)$; and the coordinates of the corners in process C would be $(P+\Delta P, V+\Delta V)$, $(P,V+\Delta V)$, $(P, V)$, and $(P+\Delta P, V)$. This would reduce the number of independent pressure and volume parameters to just three, which should simplify the math.

Also, let $$x=\frac{\Delta P\Delta V}{\left[\frac{C_v}{R}V\Delta P+\frac{C_p}{R}P\Delta V\right]}$$
In terms of this parameter, show that:
$$\eta_B=\frac{x}{\left[1-\frac{C_v}{R}x\right]}$$and
$$\eta_C=\frac{x}{\left[1+\frac{C_p}{R}x\right]}$$

 

[Andrew Mason]

Oh, I must have made a typo; the actual problem is to express the efficiency of C in terms of B. Not sure why they're labelled that way though.

I believe the heat flows $Q_{in}$ were determined correctly? I expressed the temperatures in terms of pressure, volume and $T_1$ via Charles's ($\frac{V}{T}=const.$) and Gay-Lussac's laws ($\frac{P}{T}=const.$). Then I substituted those expressions into the two equations containing the specific heat term: this can be seen in the efficiencies' denominators. I did omit a few steps in my post due to tiresome LaTeX. Do you think I have made an arithmetic mistake?

Since you are asked to compare efficiencies and since the work done in each case (Work = the area within the cycle = A) appears to be the same, this is simply a matter of comparing the Qin for each of the two cycles. How do those two heats compare? (hint: for the constant volume heating, $\Delta T \propto V\Delta P$ and for constant pressure expansion $\Delta T \propto P\Delta V$).

AM