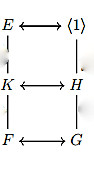The extension is Galois iff H_i is a normal subgroup of H_{i-1}

[mathmari]

Hey!

Let $E/F$ be a finite Galois extension and let the chain of extensions $F =
K_0 \leq K_1 \leq \dots \leq K_n = E$.

Let $G = Gal(E/F)$ and, for $i = 0, 1, \dots , n$, let $H_i$ be the subgroup of $G$, that corresponds to $K_i$ through the Galois mapping.

I want to show that, for any $i \in \{1, \dots, n\}$ it holds that the extension $K_i/K_{i−1}$ is Galois iff $H_i \triangleleft H_{i−1}$.
In my notes there is the following proposition:

$E/F$ is finite Galois
View attachment 6156
where $G=\text{Gal}(E/F)$

$K/F$ is normal (and so Galois) iff $H\triangleleft G$ (normal subgroup).
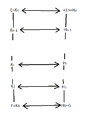
In this case we have the following:
View attachment 6157
right? (Wondering)

Can we just apply the above proposition for each $K_i/K_{i-1}$ ? (Wondering)

 

[mathmari]

Can we just apply the above proposition for each $K_i/K_{i-1}$ ? (Wondering)

Or can we not just apply this proposition and we have to do something else? (Wondering)