The Hamiltonian and Galilean transformations

[epovo]

TL;DR Summary

The effect of a coordinate transformation on the Hamiltonian is surprising (for me!)

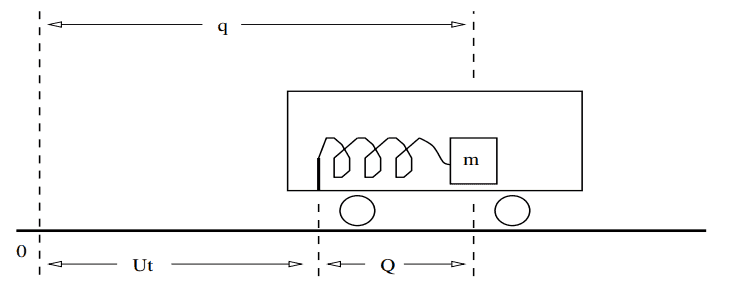
In a classical example, for a system consisting of a mass attached to a spring mounted on a massless carriage which moves with uniform velocity U, as in the image below, the Hamiltonian, using coordinate q, has two terms with U in it.
But if we use coordinate Q, $Q=q−Ut$, which moves with the carriage, the Hamiltonian, to my surprise, still contains a term in U.

$$ H=\frac 1 2 p^2/m+Up+\frac 1 2 kQ^2 $$

By choosing coordinate Q I assumed we have moved to a static frame of reference in which U can be ignored. But that does not seem to be the case.
I could calculate the Hamiltonian as if the carriage was static, and I would of course get

$$ H=\frac 1 2 P^2/m+\frac 1 2 kQ^2 $$

I am confused.

 

[anuttarasammyak]

What are definitions of p and P ? I see
$$PE=\frac{1}{2}kQ^2$$
$$KE=\frac{m}{2}(U+\dot{Q})^2$$

 

[epovo]

ok,
$$ L = \frac{m}{2}(U+\dot{Q})^2 - \frac{1}{2}kQ^2$$
$$ p = m\dot{Q} + mU $$
$$ H = \dot Q p - L = ...= \frac 1 2 p^2/m+U p+\frac 1 2 kQ^2 $$

If we ignore U completely, Kinetic Energy is simply $KE = \frac{m}{2}\dot{Q}^2$. Therefore

$$ P = \frac {\partial L} { \dot Q} = m \dot Q $$
and
$$H=\frac 1 2 P^2/m+\frac 1 2 kQ^2$$

My confusion is that the first formulation of H contains a term in U and the second one, which should be equivalent, does not. Which leads me to think of the Hamiltonian as little more than a mathematical device with no physical significance.
Either formulation leads to the same, and correct, equations of motion.

 

[anuttarasammyak]

Thanks for details. I got one of a diferent signature
$$H=\frac{p^2}{2m}-Up+\frac{k}{2}Q^2$$
which gives a equation
$$\frac{\partial H}{\partial p}=\frac{p}{m}-U=\dot{Q}$$
-Up term seems all right.

My confusion is that the first formulation of H contains a term in U and the second one, which should be equivalent, does not. Which leads me to think of the Hamiltonian as little more than a mathematical device with no physical significance.
Either formulation leads to the same, and correct, equations of motion.

The first one and the second one belong to different inertial frame of references, IFRs. Hamiltonian is not invariant under Galilean transformations.

 

[vanhees71]

Note that you have to do a canonical transformation in the Hamiltonian formalism in order to have form invariance. So let's write everything a bit more careful.

You start with phase-space coordinates $(Q,P)$. The Lagrangian reads
$$L=\frac{m}{2} (\dot{Q}+U)^2-\frac{k}{2} Q^2.$$
The canonical momentum is
$$P=\frac{\partial L}{\partial \dot{Q}}=m(\dot{Q}+U).$$
The Hamiltonian reads
$$H'(Q,P,t)=P \dot{Q}-L=m (\dot{Q}^2+U \dot{Q})-\frac{m}{2} (\dot{Q}^2+2 \dot{Q} U +U^2)+\frac{k}{2} Q^2=
\frac{m}{2} \dot{Q}^2 -\frac{m}{2} U^2 + \frac{k}{2} Q^2.$$
Now we have eliminate $\dot{Q}$ in favor of $P$:
$$H'=\frac{m}{2} (P/m-U)^2-\frac{m}{2}U^2 + \frac{k}{2} Q^2 = \frac{1}{2m} P^2 - P U + \frac{k}{2} Q^2.$$

Now you want to change to new canonical coordinates $(q,p)$ with $q=Q+U t$. So we have to find the corresponding canonical transformation. The most simple way is to find a generating function $g=g(q,P,t)$. Then
$$Q=\frac{\partial g}{\partial P}, \quad p=\frac{\partial g}{\partial q}, \quad H=H'-\frac{\partial g}{\partial t}.$$
Obviously
$$g=P(q-Ut)$$
does the job, and you get
$$H=\frac{p^2}{2m} +\frac{k}{2}(q-Ut)^2,$$
which is also what you directly get from starting with the Lagrangian
$$L=\frac{m}{2} \dot{q}^2-\frac{k}{2}(q-Ut)^2.$$

 

[epovo]

I didn't know about canonical transformations. But I thought that by making the coordinate transformation $Q=q-Ut$, I had changed my frame of reference, so that U loses its meaning and should not be part of the Lagrangian at all.

 

[vanhees71]

When you work in the Hamiltonian formulation, you must use a canonical transformation to keep the formalism form-invariant (general symplectomorphism invariance of phase space). In the Lagrangian formalism you can do arbitrary transformations of the generalized coordinates (general diffeomorphism invariance of configuration space).

In the Lagrange formalism you have
$$L=\frac{m}{2} (\dot{Q}+U)^2 + \frac{k}{2} Q^2 = \frac{m}{2} \dot{Q}^2 + \frac{k}{2} Q^2 + m \dot{Q} U +\frac{m}{2} U^2=\underbrace{\frac{m}{2} \dot{Q}^2 + \frac{k}{2} Q^2}_{L'} +\frac{\mathrm{d}}{\mathrm{d} t} \left (m QU + \frac{m}{2} U^2 t \right).$$
The Lagrangian $L'$ is thus equivalent to the Lagrangian $L$, and $L'$ is indeed independent of $U$ as it's clear from Galilei invariance.

 

[epovo]

Thank you very much @vanhees71 : That gives me peace of mind. It will probably be covered later in the text I am following, but when I saw this example I was troubled :)

 

[vanhees71]

You can also get this within the Hamiltonian formalism. Starting again from
$$H'=\frac{1}{2m} (P-mU)^2 -\frac{1}{2m} ^2 + \frac{k}{2} Q^2,$$
we look for a canonical transformation which leads to $p=P-mU$ and $q=Q$ and such as to make $H(q,p)$ independent of $U$.

We use again the generating function of the type $g(q,P,t)$. Then we have
$$Q=\frac{\partial g}{P} \stackrel{!}{=}q \; \Rightarrow \; g(q,P,t)=q P + g_2(q,t).$$
Nowe we want
$$p=\frac{\partial g}{\partial q} \stackrel{!}{=}P-mU=P+\frac{\partial g_2}{\partial q} \; \Rightarrow \; g_2(q,t)=-m U q + g_3(t).$$
Then you get
$$H=H'-\frac{\partial g}{\partial t}=\frac{1}{2m} p^2 -\frac{1}{2m} U^2 + \frac{k}{2} q^2 -\dot{g}_3.$$
So setting
$$g_3(t)=-\frac{1}{2m} U^2 t$$
we finally get
$$H=\frac{1}{2m} p^2 + \frac{k}{2} q^2.$$