The height of a section of overlapping circles.

[Zekes]

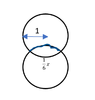
Say I have two identical circles, both of radii of one, overlapping, as shown in the diagram below:

View attachment 9059

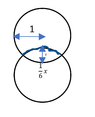
In this diagram, x is the circumference of the circles, and the bit of the bottom circle which is drawn blue (the overlapping bit) is 1/6th of the whole circumference.

What I'm looking for is y, which is this:

View attachment 9060

Now, working out x is easy - it's 2 \pi r, thus the overlapping bit is 1/3 \pi r. But how do I proceed in finding y from here? Help is much appreciated! Thanks!

 

[Greg]

Imagine a right triangle from the centre of a circle, the midpoint of the segment y and one of the points of intersection of the circles. This triangle has hypotenuse 1 and side opposite the centre of the circle 1/2. Also, this triangle is 30-60-90. Can you use some basic trig and the Pythagorean theorem to find y?

 

[Zekes]

Imagine a right triangle from the centre of a circle, the midpoint of the segment y and one of the points of intersection of the circles. This triangle has hypotenuse 1 and side opposite the centre of the circle 1/2. Also, this triangle is 30-60-90. Can you use some basic trig and the Pythagorean theorem to find y?

Although I know of trigonometry and Pythagoras, I don't see how having a point of the triangle at the midpoint of y can help me find the whole of y.

Also using some segment formulas I came up with I plugged in my values to get $$y/2=1(1-\cos ((\pi /3)/2))$$ which gives me a formula $$\approx$$ 0.133975 however this is not exact and I need an exact answer.

 

[Greg]

$$\frac{y}{2}=1-\cos30=1-\frac{\sqrt3}{2}=\frac{2-\sqrt3}{2}\implies y=2-\sqrt3$$