JimJCW
Gold Member
- 208
- 40
- TL;DR Summary
- The general form of Hubble’s law is given by, v = H(t)D, where v is the recession velocity of an object, D is the object’s proper distance from our location, and H(t) is the Hubble parameter at cosmological time t. The value of H(t) at the present time, H(now), is called the Hubble constant. Some people consider this term as a misnomer because H(t) is t-dependent. Let’s plot the H vs. t curve with Jorrie’s calculator and discuss the result. We can share our understandings and questions.
The general form of Hubble’s law for a given cosmological time t is given by,
where v is the recession velocity of an object, D is its proper distance, and H(t) is the Hubble parameter at t. To get the H vs. t plot based on the ΛCDM model, we can use the following steps:
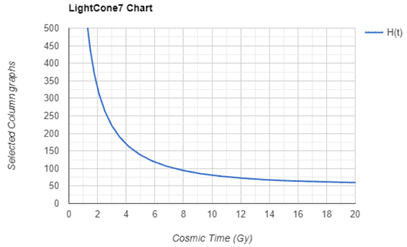
As can be seen from the above figure, H(t) had very large values during the early times of the universe. We can use Jorrie’s calculator to get the following values (1 pc = 3.26 light year):

For the present time, the Hubble law becomes,
where H(13.8) = 67.74 km/s/Mpc is called the Hubble constant. This is probably because Eq. (2) is applicable for all D values at the present time. As an example, we can calculate v for an object near the edge of the observable universe, D = 46.5 Gly. Eq. (2) gives its recession velocity as v = 3.22 c.
@Jorrie
@Bandersnatch
v = H(t)D, (1)
where v is the recession velocity of an object, D is its proper distance, and H(t) is the Hubble parameter at t. To get the H vs. t plot based on the ΛCDM model, we can use the following steps:
- Start Jorrie’s calculator: http://jorrie.epizy.com/Lightcone7-2021-03-12/LightCone_Ho7.html?i=1. It uses PLANCK Data (2015) as default input.
- Keep the default values of z(upper) and z(lower).
- Click Open Column Definition and Selection, keep only Cosmic Time and H(z) selected, and click Open Column Definition and Selection again to close it.
- Select Chart and click Calculate. The H vs. t plot will appear.
- Note: You need to use Open Chart Options to adjust the ranges of the x- and y- coordinates to get the following plot:
As can be seen from the above figure, H(t) had very large values during the early times of the universe. We can use Jorrie’s calculator to get the following values (1 pc = 3.26 light year):
For the present time, the Hubble law becomes,
v = H(13.8) D = 67.74 D, (2)
where H(13.8) = 67.74 km/s/Mpc is called the Hubble constant. This is probably because Eq. (2) is applicable for all D values at the present time. As an example, we can calculate v for an object near the edge of the observable universe, D = 46.5 Gly. Eq. (2) gives its recession velocity as v = 3.22 c.
@Jorrie
@Bandersnatch