red65
- 13
- 0
- TL;DR
- the proof of a theorem
Hello, I am studying probability and came across this theorem, it's the law of total probability with extra conditioning, I tried to work out a proof but couldn't ,does anyone know the proof for this :
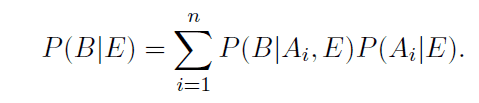
thanks!
thanks!