- #1
whatdoido
- 48
- 2
Homework Statement
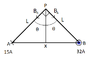
In the picture at points A and B are two thin parallel wires, where traveling currents are 15 A and 32 A to opposite directions. The distance between wires is 5.3 cm. Point's P distances from A and B are the same. Calculate the magnetic flux density at point P.
Homework Equations
##B=\mu_0\frac{I}{2\pi r}##
The Attempt at a Solution
##I_1=15A##
##I_2=32A##
##x=5.3cm=0.053m##
##\mu_0=4\pi *10^-7 Tm/A##
I solved length L with Pythagorean equation
##L^2+L^2=x^2##
##L=\frac{x}{\sqrt{2}}##
With right-hand-rule the directions of magnetic flux density can be deduced. The magnetic flux density at point P generated from point B is to the direction of point A. From point A the generated magnetic flux density at point P is towards point B.
To add both ##B_B## and ##B_A## they need to be turned downward by ##\theta## which is ##\theta=\frac{90^o}{2}=45^o##. This should be reasonable, right? The total magnetic flux density at point P is then:
##B_{total}=sin\theta B_B+sin\theta B_A=sin\theta\mu_0\frac{I_1}{2\pi \frac{x}{\sqrt{2}}}+sin\theta\mu_0\frac{I_2}{2\pi \frac{x}{\sqrt{2}}}=sin\theta(I_1+I_2)\frac{\mu_0}{\sqrt{2}\pi x}=1.773...*10^-4 T \approx 0.17mT##
This problem is from a book and it gives answer 0.19mT. I checked multiple times where I could have made a mistake but I cannot find it. The calculation is rather straightforward so there is not much to check. Thus it looks like there is some conceptual error? Thanks for reading and any help is appreciated