What is the equation for determining the magnitude of a vector in 2D space?

[CivilSigma]

Homework Statement

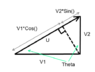
For any vector in 2D space, it can be broken down into its horizontal and vertical components.

Homework Equations

In one of my engineering classes, we are using the following equation to determine the magnitude of a vector:

$$u=v_1 \cdot cos\theta +u_2 \cdot sin\theta$$

Where $\theta$ is the angle with respect to the horizontal, v1 is the horizontal component and v2 is the vertical component of the vector.

I know this equation works but I don't understand why.
I feel like I am missing a fundamental concept, because to determine the magnitude of a vector, I would use Pythagoras theorem, and I cannot derive the above equation from Pythagoras's equation.

The Attempt at a Solution

 

[gneill]

Can you provide some context for where this equation is applied? Perhaps give a specific example.

In general, this equation will not work for a single vector whose x and y components are $u_1$ and $u_2$. Perhaps they are summing the horizontal components of two different vectors to obtain a net horizontal resultant?

 

[vela]

That equation doesn't give the magnitude of the vector. It gives you the component of the vector in the direction of $\hat n = \cos\theta\,\hat i + \sin\theta\,\hat j$.

 

[CWatters]

In one of my engineering classes, we are using the following equation to determine the magnitude of a vector:

u=v1⋅cosθ + u2⋅sinθ​

Where $\theta$ is the angle with respect to the horizontal, v1 is the horizontal component and v2 is the vertical component of the vector.

I know this equation works but I don't understand why.

It comes from geometry... See this diagram... If that's not clear do say and I will explain some more.

 

[Chestermiller]

I think you meant to write the equation as $$u=u_1\cos{\theta}+u_2\sin{\theta}\tag{1}$$where $$u_1=u\cos{\theta}\tag{2}$$and$$u_2=u\sin{\theta}\tag{3}$$If you substitute Eqns. 2 and 3 into Eqn. 1, you get:
$$u=u\cos^2{\theta}+u\sin^2{\theta}=u$$