tracker890 Source h
- 90
- 11
- Homework Statement
- Using different methods to solve for the 'maximum reversible work,' the self-solution and the answer differ, and it is unclear where the error lies.
- Relevant Equations
- Exergy balance
Energy balance
Entropy balance
Q: The maximum reversible work, self-solved, is as follows: Only when equation (5) equals zero will it match the textbook solution; kindly indicate any errors in the self-solution.
reference. : sol.; exergy balance; CMS.; wrev.
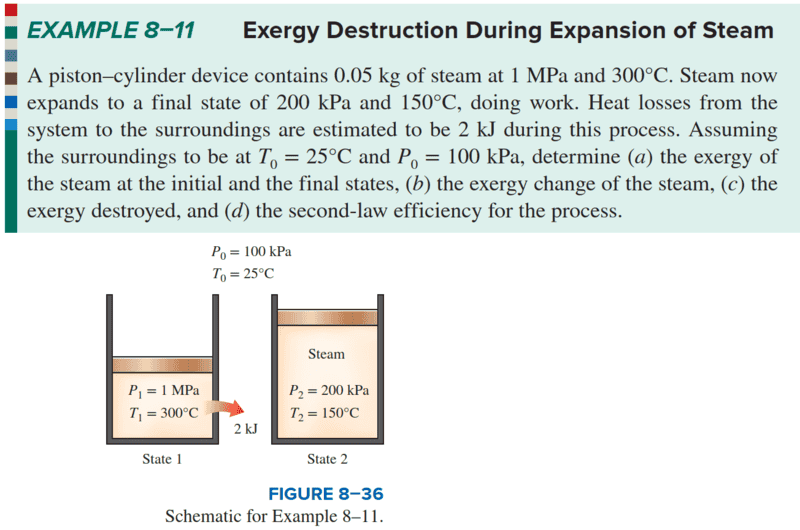
Q:
The maximum reversible work, self-solved, is as follows:
Only when equation (5) equals zero will it match the answer; please kindly point out any errors.
$$
W_{rev}=\left( W-W_{surr}^{\nearrow ^{P_0\left( V_2-V_1 \right)}} \right) +T_0Sgen\cdots \cdots \cdots \left( 1 \right)
$$
$$
eneger\ balance:\ \ Q_{in,net}^{\nearrow ^{\sum{Q_k}}}-W_{out,net}^{\nearrow ^W}=\bigtriangleup U_{sys}\cdots \cdots \cdots \left( 2 \right)
$$
$$
entropy\ balance:\ \bigtriangleup S_{sys}=\sum{\frac{Q_k}{T_k}}+\cancel{\left( \sum{m_is_i-}\sum{m_es_e} \right) }+Sgen\cdots \cdots \cdots \left( 3 \right)
$$
$$
ref.\left( 2 \right) :\ \ W=\sum{Q_k}-\bigtriangleup U_{sys}
$$
$$
ref.\left( 3 \right) :\ \ T_0Sgen=\ T_0\bigtriangleup S_{sys}-\sum{\frac{\ T_0}{T_k}}Q_k
$$
$$
\therefore W_{rev}=\sum{\left( 1-\frac{\ T_0}{T_k} \right) Q_k}-\bigtriangleup U_{sys}+T_0\bigtriangleup S_{sys}-P_0\left( V_2-V_1 \right)
$$
$$
=\sum{\left( 1-\frac{\ T_0}{T_k} \right) Q_k}+m\left[ \left( u_1-u_2 \right) -T_0\left( s_1-s_2 \right) +P_0\left( v_1-v_2 \right) \right] \cdots \cdots \cdots \left( Ans.\ W_{rev} \right)
$$
Supplement:
##m\left[ \left( u_1-u_2 \right) -T_0\left( s_1-s_2 \right) +P_0\left( v_1-v_2 \right) \right] ## same as the solution in textbook ##X_1-X_2##solution.
$$
\sum{\left( 1-\frac{\ T_0}{T_k} \right) Q_k}=Q_k^{\nearrow 2KJ}\left[ \left( 1-\frac{\ T_0^{\nearrow 298}}{T_1^{\nearrow ^{573}}} \right) +\left( 1-\frac{\ T_0^{\nearrow 298}}{T_2^{\nearrow ^{423}}} \right) \right] =0.77544^{KJ}\ne 0\cdots \cdots \cdots \left( 5 \right)
$$
reference. : sol.; exergy balance; CMS.; wrev.
Q:
The maximum reversible work, self-solved, is as follows:
Only when equation (5) equals zero will it match the answer; please kindly point out any errors.
$$
W_{rev}=\left( W-W_{surr}^{\nearrow ^{P_0\left( V_2-V_1 \right)}} \right) +T_0Sgen\cdots \cdots \cdots \left( 1 \right)
$$
$$
eneger\ balance:\ \ Q_{in,net}^{\nearrow ^{\sum{Q_k}}}-W_{out,net}^{\nearrow ^W}=\bigtriangleup U_{sys}\cdots \cdots \cdots \left( 2 \right)
$$
$$
entropy\ balance:\ \bigtriangleup S_{sys}=\sum{\frac{Q_k}{T_k}}+\cancel{\left( \sum{m_is_i-}\sum{m_es_e} \right) }+Sgen\cdots \cdots \cdots \left( 3 \right)
$$
$$
ref.\left( 2 \right) :\ \ W=\sum{Q_k}-\bigtriangleup U_{sys}
$$
$$
ref.\left( 3 \right) :\ \ T_0Sgen=\ T_0\bigtriangleup S_{sys}-\sum{\frac{\ T_0}{T_k}}Q_k
$$
$$
\therefore W_{rev}=\sum{\left( 1-\frac{\ T_0}{T_k} \right) Q_k}-\bigtriangleup U_{sys}+T_0\bigtriangleup S_{sys}-P_0\left( V_2-V_1 \right)
$$
$$
=\sum{\left( 1-\frac{\ T_0}{T_k} \right) Q_k}+m\left[ \left( u_1-u_2 \right) -T_0\left( s_1-s_2 \right) +P_0\left( v_1-v_2 \right) \right] \cdots \cdots \cdots \left( Ans.\ W_{rev} \right)
$$
Supplement:
##m\left[ \left( u_1-u_2 \right) -T_0\left( s_1-s_2 \right) +P_0\left( v_1-v_2 \right) \right] ## same as the solution in textbook ##X_1-X_2##solution.
$$
\sum{\left( 1-\frac{\ T_0}{T_k} \right) Q_k}=Q_k^{\nearrow 2KJ}\left[ \left( 1-\frac{\ T_0^{\nearrow 298}}{T_1^{\nearrow ^{573}}} \right) +\left( 1-\frac{\ T_0^{\nearrow 298}}{T_2^{\nearrow ^{423}}} \right) \right] =0.77544^{KJ}\ne 0\cdots \cdots \cdots \left( 5 \right)
$$
Last edited: