The picture of the Comoving coordinate

[Arman777]

I am trying to understand the picture of the metric in terms of the comoving coordinates but it become really confusing for me beacuse every book uses different notation for the same things.

So Let's suppose we have a flat 3D Euclidian Space, we can write the metric as,

$$dl^2 = dx^2 + dy^2 + dz^2$$ in polar form

$$dl^2 = dR^2 + R^2d\theta^2 + R^2sin(\theta)^2d\phi^2$$

Lets talk about a 2-sphere such that its radius is $R$ is constant. Then the above equation becomes

$$dl^2 = R^2d\theta^2 + R^2sin(\theta)^2d\phi^2$$

Here $R$ is the radial coordinate such that

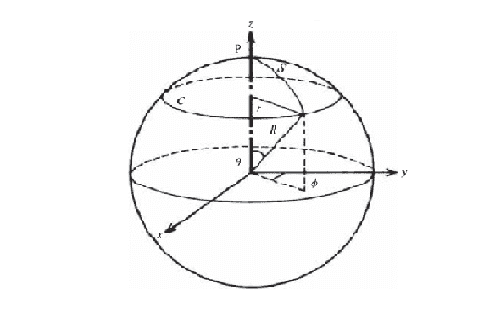
At this point if we assume that the universe is expanding we can no longer claim $dR = 0$. So let me set comoving coordinate $\sigma$ such that

$$R(t) = a(t)\sigma$$

so we can write,

$$dl^2 = a(t)^2[d\sigma^2 + \sigma^2d\theta^2 + \sigma^2sin(\theta)^2d\phi^2]$$

But this is for the flat case. In general its written as

$$dl^2 = a(t)^2[\frac{d\sigma^2}{1-k\sigma^2} + \sigma^2d\theta^2 + \sigma^2sin(\theta)^2d\phi^2]$$

There is also another comoving coordinate that we use and its generally called $\chi$. We can transform $\chi$ to $\sigma$ via

$d\chi = \frac{d\sigma}{\sqrt{1-\sigma^2}}$

And we write

$$dl^2 = a(t)^2[d\chi^2 + S_k(\chi)^2dk[d\theta^2 + sin(\theta)^2d\phi^2]]$$

Now I get confused at this point. For $k=1$ above integral becomes,

$$\chi = arcsin(\sigma)$$ or

$$\sigma = sin(\chi)$$

I am troubling to understand this geometrically.

It seems that $\chi$ is some sort of an angle. We are certain that $\sigma$ is in radial direction. So what is the $\chi$ in a geometrical sense

is it the $|AB| = \chi$ arclength. Or is it some sort of an angle such that $\angle AOB = \chi$ ?

Or is the re-scaled version of the $\sigma$ ?

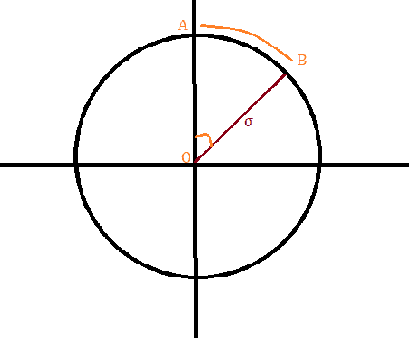
So my questions are

1)Does my equations make sense

2) If they are, where is the $\chi$ in this picture.

 

[PeterDonis]

It seems that $\chi$ is some sort of an angle.

Yes. If you want to visualize this in terms of the 2-sphere, suppose the spatial origin is at the North Pole; then $\theta$ in the usual angular coordinates (which runs from $\theta = 0$ at the North Pole to $\theta = \pi$ at the South Pole) is the analogue of $\chi$ in the 3-sphere version, and $\phi$ in the usual angular coordinates is the analogue of the 2-sphere coordinates $\theta$ and $\phi$ in the 3-sphere version. In other words, $\chi$ is an angular coordinate in the radial direction (just as, if you are standing at the North Pole on a 2-sphere, $\theta$ is an angular coordinate in your "radial" direction, the direction that points away from you).

To see the correspondence with the "scale factor" version on the 2-sphere, define a coordinate $\sigma$ such that $2 \pi R \sigma$ is the circumference of a line of latitude at radial coordinate $\sigma$. Then we can see that $\sigma = \sin \theta$.

Now take the 2-sphere metric in angular coordinates, $ds^2 = R^2 \left( d\theta^2 + \sin^2 \theta d \phi^2 \right)$, and transform it from coordinates $(\theta, \phi)$ to coordinates $(\sigma, \phi)$. We have $d \sigma = \cos \theta d \theta$, so $d\theta^2 = d\sigma^2 / \cos^2 \theta = d\sigma^2 / (1 - \sigma^2)$, and we obtain...

$$
ds^2 = R^2 \left( \frac{d\sigma^2}{1 - \sigma^2} + \sigma^2 d\phi^2 \right)
$$

...which should look familiar.

 

[Arman777]

I kind of understand but still a bit lost. So, I guess this is the correct picture ?

But by doing this we cannot write $R(t) = a(t)\sigma## ?

To see the correspondence with the "scale factor" version on the 2-sphere,

but you never used the scale factor in your equations..?

 

[PeterDonis]

I guess this is the correct picture ?

No. In your picture, we would just have $\sigma = R \chi$. That's not the equation I used (go back and check--note I used $\theta$ instead of $\chi$ for the angle you labeled as $\chi$).

you never used the scale factor in your equations..?

No, because your question actually has nothing whatever to do with the scale factor. It's just about different coordinate charts that can be used on a spacelike 3-surface. The changing scale factor can simply multiply the entire metric of the spacelike 3-surface, exactly as you do in post #1 of this thread, without affecting the form of that metric at all.

 

[Arman777]

No. In your picture, we would just have $\sigma = R \chi$. That's not the equation I used (go back and check--note I used $\theta$ instead of $\chi$ for the angle you labeled as $\chi$).
No, because your question actually has nothing whatever to do with the scale factor. It's just about different coordinate charts that can be used on a spacelike 3-surface. The changing scale factor can simply multiply the entire metric of the spacelike 3-surface, exactly as you do in post #1 of this thread, without affecting the form of that metric at all.

I see it now but Its hard to picture the $\sigma$ then. It becomes some kind of a ratio.. ? $\sigma = \rho / R$

is the analogue of $\chi$ in the 3-sphere version,

If we were talking about 3-sphere the $\chi$ would be normal radial coordinate. Maybe if you could reccomend a book I can read about these things ?

 

[PeterDonis]

It becomes some kind of a ratio.. ? \sigma=ρ/R

Yes, in other words, $\sin \chi$, or, with my labeling of the angle (I called $\theta$ what you are calling $\chi$ in the picture), $\sigma = \sin \theta$, the formula I wrote earlier.

If we were talking about 3-sphere the $\chi$ would be normal radial coordinate.

Yes, a radial angle. Which, if you're standing at the North Pole, point A in your picture, is exactly what $\chi$ is in your picture: the angle in the radial direction (the direction away from the North Pole, along a line of longitude), as opposed to the angle in the tangential direction (around a line of latitude). On a 3-sphere, you simply have two tangential angles instead of one.