The potential at points around a cone

[Identity]

Homework Statement

"A conical surface (an empty ice-cream cone) carries a uniform surface charge $$\sigma$$. The height of the cone is h, as is the radius of the top. Find the potential at the centre of the top, taking infinity as reference point." - Griffiths

My result for the potential differs from the answer's. Can someone please check my solution

Homework Equations

$$V = \iint_S \frac{1}{4\pi \epsilon_0}\frac{\sigma}{x} dS$$, where $$x$$ is the distance from the source to the point.

The Attempt at a Solution

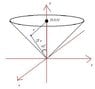
My diagram is in the attached picture.

First off, I used cylindrical coordinates with the equation z = r, z > 0 to graph the cone
I found $$dS = \sqrt{2}zdA$$

The distance from any point on the cone to the origin is $$\sqrt{2} z$$, so using the cosine law,
$$x = \sqrt{2z^2-2hz+h^2}$$

So we have

$$V = \int_0^h\int_0^{2\pi} \frac{1}{4\pi \epsilon_0} \frac{\sigma}{\sqrt{2z^2-2hz+h^2}} \sqrt{2}z d\theta dz=\frac{\sigma h}{4\epsilon}\ln(2\sqrt{2}+3)$$


Answer: $$V = \frac{\sigma h}{2\epsilon}\ln(1+\sqrt{2})$$


thanks!

 

[tiny-tim]

$$V = \int_0^h\int_0^{2\pi} \frac{1}{4\pi \epsilon_0} \frac{\sigma}{\sqrt{2z^2-2hz+h^2}} \sqrt{2}z d\theta dz=\frac{\sigma h}{4\epsilon}\ln(2\sqrt{2}+3)$$


Answer: $$V = \frac{\sigma h}{2\epsilon}\ln(1+\sqrt{2})$$

Hi Identity!

erm … 2ln(1 + √2) = ln(3 + 2√2)

 

[Identity]

oh my!
thankyou tiny-tim