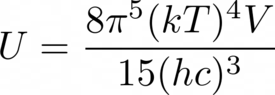The Pressure-Entropy Relationship for a Photon Gas

[Bookworm092]

Homework Statement

Given the internal energy U of a photon gas, one can take its partial derivative with respect to volume V to get the pressure P (or rather its negative). But if U is calculated by integrating Planck's distribution (see attached), then the result will not be one third of U/V, a result from kinetic theory. Please explain what has gone wrong.

Relevant Equations

See attached.

This is from Problem 7.45 of Thermal Physics by Daniel Schroeder.

 

[TSny]

Homework Statement:: Given the internal energy U of a photon gas, one can take its partial derivative with respect to volume V to get the pressure P (or rather its negative).

When taking a partial derivative, you need to specify what other variables are kept constant.

From the first law $dU = TdS - PdV$, you can see that $-P = \large \left( \frac{\partial U}{\partial V}\right)_S \;$.

 

[Bookworm092]

When taking a partial derivative, you need to specify what other variables are kept constant.

From the first law $dU = TdS - PdV$, you can see that $-P = \large \left( \frac{\partial U}{\partial V}\right)_S \;$.

Thank you for your response. I managed to crack the problem. Both $S$ and $N$ are to be kept constant. But since $T$ is not constant, I can make use of another equation to express T in terms of something else. I had already derived an expression for $S$. The answer comes out as expected from kinetic theory.

 

[vanhees71]

You cannot keep $N$ constant and varying $T$. Since "photon number" is not a conserved quantity there's no chemical potential either (despite the fact that photons are massless bosons, so that even if you could introduce a chemical potential it must be $0$ anyway).

We have given
$$U=\sigma T^4 V.$$
The "natural independent variables" for $U$ are, however $S$ and $V$ and
$$\mathrm{d}U = T \mathrm{d} S-p \mathrm{d} V.$$
From this you have
$$(\partial_S U)_V=T=\left (\frac{U}{\sigma V} \right)^{1/4}.$$
This you can integrate (using Nernst's Law that at $T=0$, where $U=0$ also $S=0$) to
$$U^{3/4}=\frac{3}{4} (\sigma V)^{-1/4} S \qquad (*)$$
or
$$U=\left (\frac{3}{4} \right)^{4/3} (\sigma V)^{-1/3} S^{4/3},$$
from which
$$p=-(\partial_V U)_S=\frac{U}{3 V}.$$
From (*) you also get the more convenient formula
$$S=\frac{4}{3} \sigma V T^3=\frac{4 U}{3T}.$$