The ratio between two horizontal speeds in this pendulum arrangement

[billtodd]

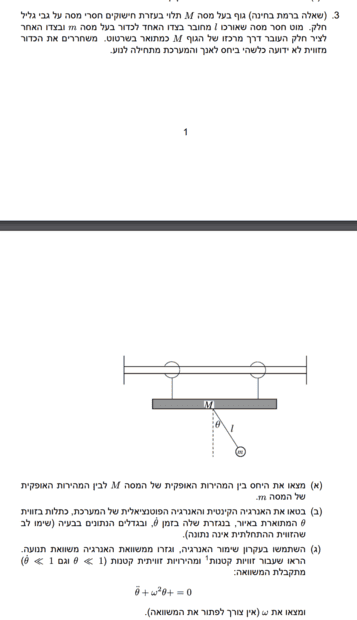
Homework Statement

To find the ratio between the horizontal speed of the stick with mass $M$ and the small point with mass $m$.

Relevant Equations

Force equation and torque.

From the forces equation I can only understand from it that the forces' equations are:$N=Mg$ and $T\sin \theta=m\ell \ddot{\theta}$.

But I don't know how to find the Torques' equations.

Any help is appreciated.


N=Mg ##Tcos⁡θ+N=mg

 

[berkeman]

Could you please type out the text from your attachment, and explain that setup? Thanks.