- #1
rasp
- 117
- 3
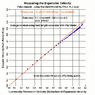
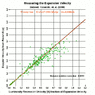
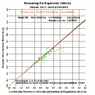
This is my 1st post ever, apologies and thanks in advance to all who read or respond. How does the actual size of all space (in linear distance dimensions) relate to the observable universe's event horizon? For example, imagine measuring out from the Earth a sphere whose radius is the event horizon (equivalent to the distance light has traveled since the Big Bang?). I imagine we would reach a particle (or observor) on the surface of that sphere, which would itself be able draw a vector length in all directions that light has traveled from it since the big bang. In one of these directions their event horizon will be a linear addition to a radius of our event horizon and will end at a third particle, which can continue the logic of viewing an event horizon in all directions. This process continued would argue for an infinite set of spheres and spatial lengths. As infinity is usually a sure sign of error, can someone explain the correct reasoning to me without using "advanced" (post college alegbra) math? Thanks kindly.