The smallest circle that two parts of a semi-circle can fit into?

[TrevorE]

So, true story:

I made a large circular tortilla.

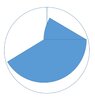
Ate half of it. Then decided to put the rest into the fridge on a smaller plate.I raised the knife to cut the remaining semi-circle in two, and then went : "Hmmmmmmmm...".

Anyway, it's in the fridge now with an approximate solution, but I'm wondering if anyone knows the mathematical one?

I'm wondering if there are 3 different optimal solutions:

1) In which the straight-line cut necessarily is from the center of the original circle to the edge. I.e. a radius.
2) In which the straight-line cut may divide the semi-circle in any possible way.
3) In which the cut is not necessarily a straight line.

Thanks in advance if anyone can offer a demonstration.View attachment 9517

 

[LCKurtz]

Next time, don't cut it that way. Instead, draw a circle on your pizza with radius $\frac r {\sqrt 2}$ and eat the annulus for your first half. You will be left with the smallest possible plate size.