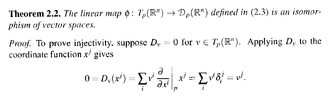The Space of All Derivations at a point p .... Tu, Theorem 2.2 .... ....

[Math Amateur]

I am reading Loring W.Tu's book: "An Introduction to Manifolds" (Second Edition) ...

I need help in order to fully understand Theorem 2.2 and the remarks after the theorem ...Theorem 2.2 and the remarks after the theorem read as follows:View attachment 8642
View attachment 8643My questions on the above text from Tu are as follows:
Question 1

At the end of the proof of the above theorem by Tu we read the following:

" ... ... This proves that $$D = D_v$$ for $$v = \langle D x^1 / ... / ... / D x^n \rangle$$ ... ..."The above implies $$v^i = D x^i$$ ... ... but what does $$D x^i$$ mean and how exactly is it equal to $$v^i$$ ... ... ?

Question 2 In some remarks after the end of the proof of the above theorem by Tu we read the following:

" ... ... Under the vector space isomorphism $$T_p ( \mathbb{R}^n ) \simeq D_p ( \mathbb{R}^n )$$, the standard basis $$e_1 \ ... \ ... \ e_n$$ for $$T_p ( \mathbb{R}^n )$$ corresponds to the set $$\partial / \partial x^1 \mid_p \ ... \ ... \ \partial / \partial x^1 \mid_p$$ of partial derivatives. From now on, we will make this identification and write a tangent vector $$v = \langle v^1 \ ... \ ... \ v^n \rangle = \sum v^i e_i$$ as

$$v = \sum v^i \frac{ \partial }{ \partial x^i } \mid_p$$ ... ... "I must say I was surprised and a little perplexed at a basis consisting of unevaluated partial derivatives ... but on reflection ... $$D_p ( \mathbb{R}^n )$$ is a space of derivations, that is linear maps satisfying the Leibniz rule ... so having a basis consisting of linear maps $$\frac{ \partial }{ \partial x^i } \mid_p$$ is not too surprising ... but how to think of a tangent vector as

$$v = \sum v^i \frac{ \partial }{ \partial x^i } \mid_p$$ ... ...is a bit of a mystery ... certainly it is hard to imagine the above quantity as an arrow at point $$p$$ ... also why we are dong this is a bit of a mystery too ...

Can someone please clarify ... ...

Hope someone can help to clarify the above issues ... ...

Peter

==========================================================================================It may help MHB readers of the above post to have access to the start of Tu's section on derivations ... so I am providing access to the same ... as follows:

View attachment 8644

Hope the above text helps with context and meaning ...

Peter

 

[GJA]

Hi Peter,

Question 1

At the end of the proof of the above theorem by Tu we read the following:

" ... ... This proves that $$D = D_v$$ for $$v = \langle D x^1 / ... / ... / D x^n \rangle$$ ... ..."The above implies $$v^i = D x^i$$ ... ... but what does $$D x^i$$ mean and how exactly is it equal to $$v^i$$ ... ... ?

$D$ is a chosen derivation from $\mathcal{D}_{p}(\mathbb{R}^{n}).$ It is a real-valued linear functional from $C^{\infty}_{p}$ to $\mathbb{R}.$ Each of the coordinate functions $x^{1}, x^{2}, \ldots, x^{n}$ (defined by $x^{j}(p) = p^{j}$) belongs to $C^{\infty}_{p}.$ $Dx^{i}$ is the real number obtained when $D$ acts on $x^{i}$. Call this number $c^{i}$ if it helps.

At this point in the proof Tu is trying to show that $\phi$ is surjective. This means we must find a $v$ in $T_{p}(\mathbb{R}^{n})$ that $\phi$ maps to $D$. Tu is showing that by setting $v=(Dx^{1}, Dx^{2}, \ldots, Dx^{n})= (c^{1}, c^{2}, \ldots, c^{n})$ (i.e., defining $v^{i}=c^{i}=Dx^{i}$), we obtain a vector whose image under $\phi$ is $D$. Hence, $\phi$ is onto.

I must say I was surprised and a little perplexed at a basis consisting of unevaluated partial derivatives ...

Is it a concern to say that we have a smooth function $f$ from the set $C^{\infty}_{p}$? The function $f$ as written is not evaluated at any point, yet there is likely little/no apprehension when it appears. There is no difference between $\frac{ \partial }{ \partial x^i }$ being unevaluated and $f$ being unevaluated. The only caveat being the former's domain are smooth functions and the latter's are points in $\mathbb{R}^{n}$.

... but how to think of a tangent vector as

$$v = \sum v^i \frac{ \partial }{ \partial x^i } \mid_p$$ ... ...is a bit of a mystery ... certainly it is hard to imagine the above quantity as an arrow at point $$p$$

The isomorphism established means that you can think of it as an arrow if you wish. Admittedly, this can be very useful when trying to understand things from a more intuitive approach.

Rigorously speaking, however, you are to think of a tangent vector as a linear operator because that is now what it is defined to be (which we discussed in your previous post). The equation $$v = \sum v^i \frac{ \partial }{ \partial x^i } \mid_p$$ indicates that the operators $\frac{ \partial }{ \partial x^i } \mid_p$ are a basis for the tangent space at $p$; i.e., any linear operator = tangent vector at $p$ can be written as a linear combination of the $\frac{ \partial }{ \partial x^i } \mid_p$.

A useful exercise may be to draw a vector on a sheet of paper and tell yourself this is not just an arrow, it is also an operator that represents the directional derivative of a smooth function in the direction the arrow points in.

... also why we are dong this is a bit of a mystery too ...

As we discussed in the other post, the reason we are doing this is because a general manifold must be considered an object in its own right and not as a subset of some ambient $\mathbb{R}^{n}$ space. Because we cannot rely on our intuition from $\mathbb{R}^{n}$ to form a rigorous theory, we cannot define tangent vectors as arrows. This is why this is abstract mathematics. We must not rely on our intuition anymore. Instead, we must extract properties possessed by the intuitive notion of a vector to create an abstract definition of what a vector is, thereby extending the utility of a tangent vector far beyond the realm of just $\mathbb{R}^{n}.$ Using the interpretation of vectors as linear operators (via their use in calculating directional derivatives), the rigorous definition of a tangent vector is that it is a linear operator. The isomorphism theorem quoted and all of Chapter 2 of Tu's book are trying to convince us that the transition from arrows to linear operators is the most natural extension of the vector concept one can define in an abstract setting.

 

[Math Amateur]

Hi Peter,
$D$ is a chosen derivation from $\mathcal{D}_{p}(\mathbb{R}^{n}).$ It is a real-valued linear functional from $C^{\infty}_{p}$ to $\mathbb{R}.$ Each of the coordinate functions $x^{1}, x^{2}, \ldots, x^{n}$ (defined by $x^{j}(p) = p^{j}$) belongs to $C^{\infty}_{p}.$ $Dx^{i}$ is the real number obtained when $D$ acts on $x^{i}$. Call this number $c^{i}$ if it helps.

At this point in the proof Tu is trying to show that $\phi$ is surjective. This means we must find a $v$ in $T_{p}(\mathbb{R}^{n})$ that $\phi$ maps to $D$. Tu is showing that by setting $v=(Dx^{1}, Dx^{2}, \ldots, Dx^{n})= (c^{1}, c^{2}, \ldots, c^{n})$ (i.e., defining $v^{i}=c^{i}=Dx^{i}$), we obtain a vector whose image under $\phi$ is $D$. Hence, $\phi$ is onto.
Is it a concern to say that we have a smooth function $f$ from the set $C^{\infty}_{p}$? The function $f$ as written is not evaluated at any point, yet there is likely little/no apprehension when it appears. There is no difference between $\frac{ \partial }{ \partial x^i }$ being unevaluated and $f$ being unevaluated. The only caveat being the former's domain are smooth functions and the latter's are points in $\mathbb{R}^{n}$.
The isomorphism established means that you can think of it as an arrow if you wish. Admittedly, this can be very useful when trying to understand things from a more intuitive approach.

Rigorously speaking, however, you are to think of a tangent vector as a linear operator because that is now what it is defined to be (which we discussed in your previous post). The equation $$v = \sum v^i \frac{ \partial }{ \partial x^i } \mid_p$$ indicates that the operators $\frac{ \partial }{ \partial x^i } \mid_p$ are a basis for the tangent space at $p$; i.e., any linear operator = tangent vector at $p$ can be written as a linear combination of the $\frac{ \partial }{ \partial x^i } \mid_p$.

A useful exercise may be to draw a vector on a sheet of paper and tell yourself this is not just an arrow, it is also an operator that represents the directional derivative of a smooth function in the direction the arrow points in.
As we discussed in the other post, the reason we are doing this is because a general manifold must be considered an object in its own right and not as a subset of some ambient $\mathbb{R}^{n}$ space. Because we cannot rely on our intuition from $\mathbb{R}^{n}$ to form a rigorous theory, we cannot define tangent vectors as arrows. This is why this is abstract mathematics. We must not rely on our intuition anymore. Instead, we must extract properties possessed by the intuitive notion of a vector to create an abstract definition of what a vector is, thereby extending the utility of a tangent vector far beyond the realm of just $\mathbb{R}^{n}.$ Using the interpretation of vectors as linear operators (via their use in calculating directional derivatives), the rigorous definition of a tangent vector is that it is a linear operator. The isomorphism theorem quoted and all of Chapter 2 of Tu's book are trying to convince us that the transition from arrows to linear operators is the most natural extension of the vector concept one can define in an abstract setting.

Thanks for a most helpful post, GJA ...

With your help I might end up understanding manifolds!

I really appreciate your help ...

Peter