The value of "k" for spring constant, is the book answer incorrect?

In summary, the conversation revolves around solving a Hook's law problem for the values of Fi and k. The given data shows a linear relationship between applied force and displacement, with a value of 50lb/in for k. Some individuals have tried different methods to solve the problem, but the simplified equation of Δy = ΔF/k seems to provide the most straightforward solution. This information is provided in the textbook as well.
  • #1
SShep71
5
0
Homework Statement
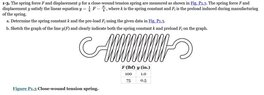
1-3. The spring force F and displacement y for a close-wound tension spring are measured as shown in Fig. P1.3 The spring force and displacement satisfy the linear equation y=((1/k)F-(Fi/k)
, where k is the spring constant and Fi is the preload induced during manufacturing of the spring.

(a) Determine the spring constant k and the pre-load F using the given data in Fig. P1.3. (b) Sketch the graph of the line y(F) and clearly indicate both the spring constant k and preload Fi using the given data.
Relevant Equations
y=((1/k)F-(Fi/k))
There is some discussion currently and I was hoping to get some opinions here. The question is in regard to a Hook's law problem. The text gives the problem as seen below. The text says the answer is 50lb/in. Several people have tried from several different approaches. Factoring the "y" equation to solve for Fi, straight method, etc.

In case the image does not work, here are the specifics:
k= spring constant
Fi=preload at manufacturing
F=spring force
y=displacement

Observations:
F(lbf) y(in)
100 1.0
75 0.5

The students are to determine the "Fi" and "k" values. The book states 50lb/in as the answer
 

Attachments

  • spring.JPG
    spring.JPG
    31.3 KB · Views: 95
Physics news on Phys.org
  • #2
SShep71 said:
Observations:
F(lbf) y(in)
100 1.0
75 0.5

The students are to determine the "Fi" and "k" values. The book states 50lb/in as the answer
If the relationship between (total) applied force and (total) displacement is linear, then (using that data) an additional extension of 0.5 inches requires an additional force of 25 lbf. Hence ##k = 50## lbf per inch.
 
  • #3
No disagreement from me, the logic is sound. I guess it's the method of algebraically solving it that seems to have a few "twisted-under britches" in this group.
 
  • #4
SShep71 said:
No disagreement from me, the logic is sound. I guess it's the method of algebraically solving it that seems to have a few "twisted-under britches" in this group.
Note that your relevant equation:

Relevant Equations: y=((1/k)F-(Fi/k))

Can be simplified to:
$$\Delta y = \frac{\Delta F}{k}$$Which may help to straighten out your britches.
 
  • Haha
Likes berkeman

FAQ: The value of "k" for spring constant, is the book answer incorrect?

What is the spring constant "k" and how is it defined?

The spring constant "k" is a measure of a spring's stiffness. It is defined by Hooke's Law, which states that the force exerted by a spring is directly proportional to the displacement from its equilibrium position. Mathematically, it is expressed as F = -kx, where F is the force applied, x is the displacement, and k is the spring constant.

How can I determine if the book answer for "k" is incorrect?

To verify the book answer for "k," you can perform an experiment to measure the force and displacement, then calculate "k" using Hooke's Law (k = F/x). Compare your experimental value with the book's value. Additionally, check if the book provides sufficient context and correct units for the spring constant.

What units are used for the spring constant "k"?

The spring constant "k" is typically measured in Newtons per meter (N/m) in the International System of Units (SI). This unit signifies the amount of force required to displace the spring by one meter.

Can the value of "k" vary for the same spring?

The value of "k" should remain constant for a given spring under ideal conditions. However, factors such as temperature changes, material fatigue, and deformation beyond the elastic limit can cause variations in the spring constant.

What could cause discrepancies between the experimental value of "k" and the book answer?

Discrepancies can arise from experimental errors, such as inaccurate measurements of force or displacement, or using a spring that has been damaged or altered. Additionally, differences in environmental conditions or assumptions made in the book (e.g., ideal vs. real-world conditions) can lead to varying values of "k."

Similar threads

Energy stored in a double spring system
Replies
17
Views
814
Spring Problem Involving Variables and Constants Only
Replies
3
Views
877
Multiple choice Q: Mangetic fields and Spring Constant
Replies
8
Views
2K
Equations of Motion for Pulley System with Belt and Spring Constants
Replies
1
Views
1K
Problem with solving for force constant k of spring?
Replies
3
Views
2K
Trouble understanding the influence of a real spring in a system
Replies
3
Views
1K
How Do You Apply Laplace Transforms to Vehicle Suspension Analysis?
Replies
6
Views
3K
Hooke's Law Lab Spring Constant Calculation
Replies
3
Views
2K
Maximum displacement in mass spring system
Replies
5
Views
2K
Need to find the spring constant to achieve Max Velocity
Replies
6
Views
1K

Hot Threads

Recent Insights

Back
Top