Therefore, the roots of the given equation are $x=-4$ and $x=2$.

So the two roots are $x=-4$ and $x=2$. In summary, to solve the equation (x+3)^2 = 4x+17, you can either use the cross method or the zero-factor property. However, in the second method, it is important to make sure the signs are correct when factoring the quadratic. In this case, the correct roots are x=-4 and x=2.
  • #1
led
1
0
Solve (x+3)^2 = 4x+17 where did i go wrong?
(x+3)(x+3 )= 4x+17

x^2 + 3x + 3x + 9 = 4x+17

x^2 + 6x + 9 = 4x + 17

x^2 + 6x + 9 - 4x - 17 = 0

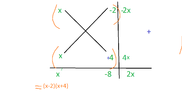
x^2 + 2x - 8 = 0

(x-2)(x+4) <-- USING THE CROSS METHOD View attachment 3985

x= -2, 4 is my cross method working incorrect or something? do explain my mistake
 

Attachments

  • math.png
    math.png
    7.3 KB · Views: 68
Mathematics news on Phys.org
  • #2
led said:
where did i go wrong?
In the very last line. Well, second last line.
 
  • #3
You have factored correctly, but your roots have the wrong signs.

Another method to solve this equation would be to write it as:

\(\displaystyle (x+3)^2-4x-17=0\)

\(\displaystyle (x+3)^2-4(x+3)-5=0\)

Now factor the quadratic in $x+3$:

\(\displaystyle \left((x+3)+1\right)\left((x+3)-5\right)=0\)

Combine like terms:

\(\displaystyle (x+4)(x-2)=0\)

Now, to find the actual roots, use the zero-factor property, and equate each factor to zero in turn and solve for $x$:

\(\displaystyle x+4=0\implies x=-4\)

\(\displaystyle x-2=0\implies x=2\)
 

FAQ: Therefore, the roots of the given equation are $x=-4$ and $x=2$.

What is a quadratic equation?

A quadratic equation is an algebraic equation of the form ax^2 + bx + c = 0, where a, b, and c are constants and x is the variable. It can also be written in the form of y = ax^2 + bx + c, where y is the dependent variable and x is the independent variable.

What is the general solution to a quadratic equation?

The general solution to a quadratic equation is given by the quadratic formula, which is x = (-b ± √(b^2 - 4ac)) / 2a. This formula gives the two possible values of x that satisfy the quadratic equation.

What is the discriminant of a quadratic equation?

The discriminant of a quadratic equation is the expression b^2 - 4ac, which appears under the square root in the quadratic formula. It helps determine the nature of the roots of a quadratic equation.

How do I solve a quadratic equation without using the quadratic formula?

There are multiple methods for solving a quadratic equation without using the quadratic formula, such as factoring, completing the square, and graphing. The method used will depend on the form of the equation and personal preference.

What are the real-life applications of quadratic equations?

Quadratic equations have many real-life applications, such as in physics to calculate the trajectory of a projectile, in engineering to design bridges and buildings, and in business to model profit and cost functions. They are also used in various fields of science and technology.

Similar threads

MHB Which Quadratic Function Has Exactly One X-Intercept?
Replies
3
Views
2K
MHB Solve Equation: $x^4+2x^3-x^2-6x-3=0$
Replies
7
Views
1K
MHB Can graph be used to solve inequalities without algebra?
Replies
2
Views
1K
MHB Value of k in definite Integration
Replies
1
Views
1K
MHB Fixed point,, Jacobi- & Newton Method, Linear Systems
Replies
7
Views
2K
MHB Absolute Value Equation |3x - 2|/|2x - 3| = 2
Replies
10
Views
2K
MHB [ASK] A Line Intercepting A Circle
Replies
4
Views
1K
MHB How can you solve $5^{x^2+8}=125^{2x}$ for x?
Replies
8
Views
1K
MHB How to Evaluate the Infinite Sum for 0 < x < 1?
Replies
6
Views
2K
B Need assistance with an unusual quadratic solution method
Replies
4
Views
1K

Hot Threads

Recent Insights

Back
Top