Three equal charges are situated at the vertex of an equilateral

[Telemachus]

Hi there. I did this problem, and I wanted to know if my solution is ok.

The problem says: Three equal charges are situated at the vertex of an equilateral triangle, and we want to cancel out the forces exerted by each other. What charge q' of opposite sign should be placed at the center of the triangle?

I've made a picture:

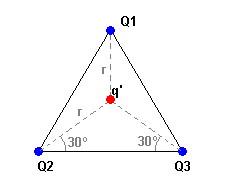
The side of the triangle: $$l=2r\cos 30º=\sqrt[ ]{3}r$$
And the height: $$h=r+r\sin 30º=\displaystyle\frac{3}{2}r$$

Then I set the force summatory for Q2.

$$\vec{F_2}=\displaystyle\frac{Q_2}{4\pi \epsilon_0}\left ( \frac{4Q_1}{9r^2}\hat{j}+\frac{4Q_1}{3r^2}\hat{i}+\frac{Q_3}{r^2}\hat{i}-\frac{4q'}{r^2}\hat{j}-\frac{4q'}{3r^2}\hat{i} \right)$$

Under the conditions:
$$\vec{F_2}=0,Q_1=Q_3=Q$$

I get:
$$q'\hat{i}=\displaystyle\frac{7}{4}Q\hat{i},q'\hat{j}=\displaystyle\frac{Q}{9}j$$

Then $$||q'||\approx{}1.75Q$$

And then: $$q'\approx{1.75Q}$$

Is this right?

 

[Delphi51]

Curious, I get a slightly different answer and haven't the patience to check through your 2D calc. Consider this ...
The force on Q2 due to Q1 is F = kQ²/(3r²).
Q3 on Q2 is the same and components perpendicular to q'Q2 cancel, so double and use cos(30) to get the components parallel to q'Q2 (left side), which must be equal to the q'Q2 force (right side):
2*kQ²/(3r²)*cos(30) = kQq'/r²
just cancelling ...
2/3*Q*cos(30) = q'
0.577*Q = q'

 

[Telemachus]

Thank you very much Delphi. Is something wrong about my reasoning? without getting into details on my decomposition in Cartesian coordinates. What I did was, from the equation for the summatory of forces:

$$\displaystyle\frac{4Q_1}{9r^2}\hat{j}+\frac{4Q_1}{3r^2}\hat{i}+\frac{Q_3}{r^2}\hat{i}-\frac{4q'}{r^2}\hat{j}-\frac{4q'}{3r^2}\hat{i}=0$$

Then, separating into the different components, and computing the modulus I get into my result.

I want to know if my conception was right, it doesn't matter if I made a mistake when making the decomposition over i and j, but I do care if I reasoned this wrong.

 

[lewando]

I think you might have a problem somewhere in here:

Then I set the force summatory for Q2.

$$\vec{F_2}=\displaystyle\frac{Q_2}{4\pi \epsilon_0}\left ( \frac{4Q_1}{9r^2}\hat{j}+\frac{4Q_1}{3r^2}\hat{i}+\frac{Q_3}{r^2}\hat{i}-\frac{4q'}{r^2}\hat{j}-\frac{4q'}{3r^2}\hat{i} \right)$$

At Q₂, you can argue that the forces in the x direction must equal 0, as well as the forces in the y direction. So, taking just the x direction:
$$\vec{F_2x}=\displaystyle\frac{Q_2}{4\pi \epsilon_0}\left ( \frac{-cos(60)Q_1}{3r^2}\hat{i}-\frac{Q_3}{3r^2}\hat{i}+\frac{cos(30)q'}{r^2}\hat{i} \right)$$

$$0=\displaystyle \frac{-cos(60)Q}{3}-\frac{Q}{3}+\frac{cos(30)q'}{1}$$

which results in the answer Delphi51 got (which is 1/3rd of what you got).

 

[Telemachus]

Thank you very much sir :), I'll review this later with more time (I have to go to school right now) but I think you got it.