Three inertial particles: Separating the twins from the paradox

[Trysse]

TL;DR Summary

I model the twin paradox with a straightedge and a compass.
To do this, I take the nonchalant trope that "the formula of the spacetime interval is like the formula of the Pythagorean theorem but with a minus sign" literally.

This is a response to a recent insight article regarding the twin paradox. The idea is to model the most basic scenario in a way, that the paradox disappears. This basic scenario and its kinematic effects are then modeled using only a straightedge and a compass.

The best way to read this post is to have a pen, paper, a compass, and a straightedge ready. Alternatively, the construction can be done in programs such as GeoGebra. The geometrically minded may also do the geometry in their head. For those with little geometric imagination, I provide a complete drawing at the end of the post that you can use for reference. However, I encourage you to really "do the geometry".

Before I model the twin paradox, I first strip the scenario of all elements that are usually part of the narrative. This includes the story of two twins, that are separated and reunited having aged differently. Secondly, I remove all references to observations (i.e. that one of the twins sees the other twin). Next, I remove all technical gimmicks such as rocket ships or telescopes that are used to flesh out the story. I will also remove something that might be unsuspicious of adding confusion: coordinate systems, coordinates, and frames of reference. Instead, I will model a spatial geometry on which observers who are embedded in this geometry must apply their relativistic coordinate systems. Lastly, I will remove the paradox from the title of the scenario: Instead of Twin Paradox, I name it the “three inertial particles scenario”.

In this scenario, I consider three particles $P_1$, $P_2$, and $P_3$ at three distinct events $A$, $B$, and $C$. The events take place in a space without significant gravitational effects. For this model, an event is the coincidence of two particles in one place. To be in one place means, that two particles collide or pass each other very close. In this model, every event creates an electromagnetic signal. A signal propagates outward from the location of the event at constant speed in all directions. The three events are time-like related. This is what happens at and between the events:

At the first event $A$, the particles $P_1$ and $P_3$ coincide.
After event $A$, the particles $P_1$ and $P_3$ move in different directions.
Particle $P_1$ moves in the direction where the event $B$ will take place.
Particle $P_3$ moves in the direction where the event $C$ will take place.
At the second event $B$, the particles $P_1$ and $P_2$ coincide.
After event $B$, the particle $P_2$ moves on a trajectory that will eventually intercept particle $P_3$ at the event $C$.
At the third event $C$, the particles $P_2$ and $P_3$ coincide.

The model aims to determine the proper time the particles experience between the different events.

The particle $P_1$ experiences a proper time of $t_1$ between the events $A$ and $B$.
The particle $P_2$ experiences a proper time of $t_2$ between the events $B$ and $C$.
The particle $P_3$ experiences a proper time of $t_3$ between the events $A$ and $C$.

To relate this scenario to the original "twin paradox" I compare the proper time $t_3$ with the combined proper time $t_1 + t_2$.

In the intervals, $AB$, $BC$, and $AC$ between the events, the respective particles experience no acceleration. However, before or after the interval and at each event the particle may experience acceleration. This process of staging the particles for the three events is not part of the description.

If you do not yet have a compass and straightedge or GeoGebra ready, I urge you to do so. If you have time to spare, you should stop here and think for yourself how to draw the above scenario just with a compass and a straightedge. To prevent you from accidentally reading ahead, I have hidden further explanations behind the different spoiler buttons:

Hints
Modeling procedure,
related geometric concepts and graphical inspiration
Drawing and GeoGebra models

The first section "Hints" gives you just three very basic hints, which don't give away too much of the model.

The second section "Modelling procedure" is a complete step-by-step guide. I explain how to model the above scenario. If you just read this section you risk the feeling of disappointment that you did not even try to come up with the model yourself.

The third section "Related geometric concepts and graphical inspiration" can be read in two ways:
1) If you are not able to come up with a model by yourself you can read this section to get inspiration.
2) If you have either come up with the model by yourself or have read the previous section, you can check, if you can identify the related concepts before reading the section.

The final section "Drawing and GeoGebra models" contains just that: A drawing and links to two different GeoGebra models. Here you can check if your model is the same as mine without going through the complete modeling procedure.

Spoiler: Basic Modelling hints

If you decide to try and draw your own model, I give you three hints:

1) The idea is not to draw a Minkowski spacetime diagram.
2) The model requires only one drawing.
3) Since the three points are always coplanar, I can restrict the model to a plane without losing any relevant degree of freedom.

Spoiler: Modelling Procedure

This is how I model:

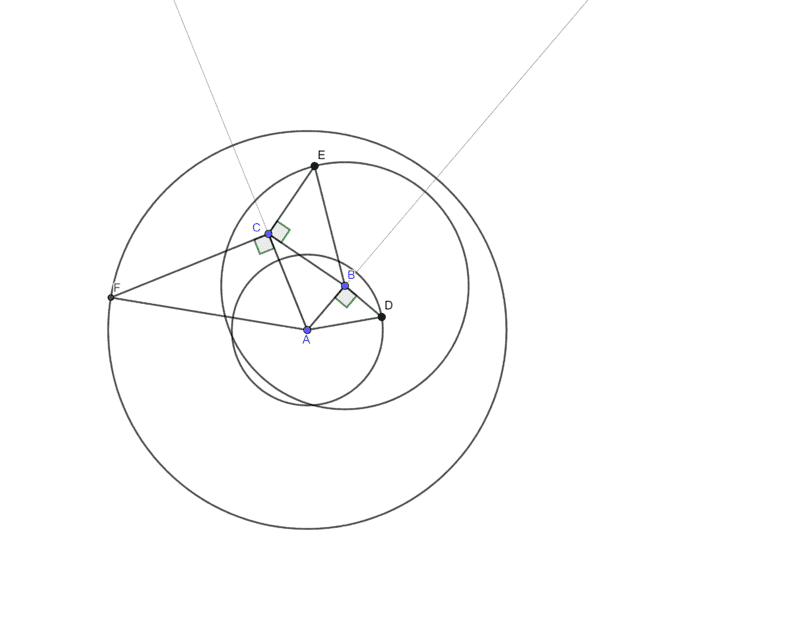
I mark a point $A$ on the plane. From this point, I draw two rays $b$ and $c$ in arbitrary directions. Point $A$ marks the location where the particles $P_1$ and $P_3$ coincide (i.e. the event A). The two rays mark the directions of the particles $P_1$ and $P_3$ after event $A$ has taken place.

Next, I mark a second point $B$ that lies on one of the ray $b$. This point marks where the particles $P_1$ and $P_2$ coincide (i.e. the event $B$). The distance $AB$ is the spatial separation between events $A$ and $B$.

In the next step, I model the temporal separation between the events. This temporal separation literally answers the question: How long after event $A$ does event $B$ take place? For this, I draw a circle $c_1$ around point $A$. The radius $r_1$ of this circle must be greater than the distance between points $A$ and $B$ (i.e. $r_1 > AB$). This circle signifies how far the electromagnetic signal emitted in the event $A$ propagates while the particle $P_1$ moves from $A$ to $B$. If the radius of the circle is much larger than the distance $AB$, the particle $P_1$ moves much slower than the signal propagates. The smaller the radius, the faster the particle moves. The speed of the particle can be expressed as $v_1=AB \div r_1$. It should be noted, that this “speed” is a dimensionless ratio: The numerator (i.e. the distance $AB$) and the denominator (i.e. $r_1$) of the ratio are both distances.

After modeling the spatial and temporal separation, I can determine how much proper time $t_1$ the particle $P_1$ experiences as it moves from $A$ to $B$: I apply the two distances $AB$ and $r_1$ to the formula of the spacetime interval:

$$\Delta s^2 =\Delta t^2 - \Delta x^2$$

Because the events $A$ and $B$ are time like related, I can plug in $s = t_1$, $\Delta t = r_1$ and $\Delta x = AB$. If I draw the square root, I get

$$t_1 =\sqrt{(r_1)^2 - (AB)^2}$$

The question is: Which distance or distances in the drawing represent (the square root of) the spacetime interval? If you don't see it immediately take your time. Draw some line segments. I will point it out in the next step. But once I tell it to you, the relation becomes obvious. Then the possibility for your own "aha moment" is gone.

To represent $t_1$ I draw a line segment that starts in point $B$ and that is perpendicular to the line segment $AB$. The endpoint of this line segment lies on the circumference of the circle $c_1$. It is not important to which side I draw this line segment. For reference, I will name the point where the line segment touches the circle $c_1$ point $D$. I now have a right-angled triangle $ABD$. The side $AB$ is the distance between the locations at which the two events take place. The side $AD$ of this triangle is the radius of the circle i.e. $r_1$ the distance the signal has propagated. This side $AD$ is obviously the hypothenuse of the triangle! The side $BD$ is the side for which the formula of the spacetime interval applies.

It is important to note, that the point $D$ and the line segments $AD$ and $BD$ have no spatial significance. Nothing moves along those line segments, nothing happens at point $D$. The lengths of the line segments abstractly represent physical quantities: The line segment $AD$ represents the distance the signal has propagated (in all directions not only along the line segment). The length of the line segment $BD$ is proportional to the proper time that can be read of a clock moving with particle $P_1$. I.e. $BD = t_1$.

If the distance $AB$ is one light second, then $t_1 = (BD \div AB) seconds$.

I can now repeat the same procedure for the particle $P_2$ and the interval $BC$: First, I mark a point $C$, that lies on the second ray $c$. This point $C$ marks where the particle $P_2$ and $P_3$ coincide. I can connect points $B$ and $C$ with a line segment to visualize the trajectory of the particle $P_2$. Next, I draw a circle $c_2$ with a radius $r_2 > BC$ around the point $B$. I draw a line segment from point $C$, that is perpendicular to $BC$ and that ends on the circumference of the circle $c_2$. I name the point where the line segment and the circle meet $E$. I have again a rightangled triangle $BCE$ The distance $CE$ represents the proper time $t_2$ that the particle $P_2$ experiences between the two events $B$ and $C$.

The question is now: How much proper time $t_3$ does the particle $P_3$ experience between the two events $A$ and $C$? The time that the particle experiences depends on the distance $AC$ and on the distance the electromagnetic signal from the event $A$ has propagated as the event $C$ takes place.

I know that the signal from the event $A$ propagates the distance $AD$ while the particle $P_1$ moves from $A$ to $B$. After event $B$ the signal propagates the distance $BE$, while the particle $P_2$ moves from $B$ to $C$. So, I can conclude, that between the events $A$ and $C$, the signal from event $A$ propagates a total distance of $AD + BE$. Consequently, I draw a circle around the point $A$ with a radius $r_3 = AD + BE$. Next, I draw a line segment that starts in point $C$, that is perpendicular to $AC$ and that ends on the circumference of the circle $c_3$. I name this point $F$. I have again a right-angled triangle ACF. The distance $CF$ expresses the proper time $t_3$, the particle $P_3$ experiences between the events $A$ and $C$.

You can create different variations of this model and see, how the proper times $t_1 + t_2$ (i.e. $BD + CE$) and $t_3$ (i.e. $CF$) relate to each other.

If I assign a numerical value to $t_1$, I can calculate $t_2$, $t_3$ and the distances.

By replacing all circles with spheres, I can imagine the above scenario in a voluminous space. However, for visualization, it is easier to stick to a plane. If I look at the model on a plane, it is as if I look into a Minkowski spacetime diagram from the top.

In a way this model is lazy. It tacitly assumes, that there are clocks inside the particles that somehow register “the passage of time” without considering what that means. However, this laziness is due to the need to keep the model clear and simple. I could model the particles as moving light clocks in which electromagnetic signals propagate up and down or forward and backward. The distances $BD$, $CE$, and $CF$ express the proper distance that electromagnetic signals “move around” within the particles as the particles traverse the spatial separation between two events. If the particles are modeled to this level of detail, it is necessary to model particles contracted along their direction of movement.

Spoiler: Related geometric concepts and graphical inspiration

In this model, the spacetime interval between two events is related to the concept of the power of a point as introduced by Swiss mathematician Jacob Steiner in 1826.

On a more fundamental level, the spatial representation of the spacetime interval is related to the theorems of intersecting chords and intersecting secants

The visualization is inspired by the works of French scientist Étienne-Jules Marey. Especially his studies of motion.

Spoiler: Drawing and GeoGebra models

Drawing of the three particle scenario as described above:

Basic GeoGebra model: https://www.geogebra.org/classic/u99bxf5p
Animated https://www.geogebra.org/classic/pzgjv6qv

Spoiler: Simplicity and objections

This model is simple. It is literally as simple as $a^2 + b^2 = c^2$ or rahter $a^2 = c^2 - b^2$. It is so simple, that everybody who knows the math of SR kinematics could have come up with it. However, simplicity doesn't imply that it is a good or even a true model.
I am aware of the objections that can be brought up against this model. However, I leave it to others to bring forward these objections.
Regardless of whether you think this model is good or bad, true or false, I hope you can at least enjoy the model for its simplicity.

 

[vanhees71]

I never understood why one thinks that it helps to invent ever more complicated scenarios to resolve an apparent paradox although it's very simple in principle. Due to the relativistic spacetime model (Minkowski space for special relativity) being different from the Galilean spacetime model in Newtonian mechanics, ideal clocks always show their proper time, i.e., when comparing two clocks being set to $0$ at a common place at another common place at later time, the two show different times, because their proper times are a functional of the time-like worldlines. The proper time of each clock is given by
$$\tau=\int_0^{t} \mathrm{d} t' \sqrt{1-\dot{\vec{x}}(t')^2},$$
where $t$ is the "coordinate time" in an arbitrary fixed "computational inertial frame of reference". For different worldlines $x_1(t')=(t,\vec{x}_1(t'))$ and $x_2(t)=(t,\vec{x}_2(t'))$, where $(\vec{x}_1(0)=\vec{x}_2(0)$ and $\vec{x}_1(t)=\vec{x}_2(t)$ obviously in general the proper times of the two clocks will show different times, which are in general also different from $t$.

So there's no more paradoxical in this situation as in standard Euclidean geometry two curves connecting the same two points have in general different lengths.

 

[FactChecker]

I never understood why one thinks that it helps to invent ever more complicated scenarios to resolve an apparent paradox although it's very simple in principle. Due to the relativistic spacetime model (Minkowski space for special relativity) being different from the Galilean spacetime model in Newtonian mechanics, ideal clocks always show their proper time, i.e., when comparing two clocks being set to $0$ at a common place at another common place at later time, the two show different times, because their proper times are a functional of the time-like worldlines. The proper time of each clock is given by
$$\tau=\int_0^{t} \mathrm{d} t' \sqrt{1-\dot{\vec{x}}(t')^2},$$
where $t$ is the "coordinate time" in an arbitrary fixed "computational inertial frame of reference". For different worldlines $x_1(t')=(t,\vec{x}_1(t'))$ and $x_2(t)=(t,\vec{x}_2(t'))$, where $(\vec{x}_1(0)=\vec{x}_2(0)$ and $\vec{x}_1(t)=\vec{x}_2(t)$ obviously in general the proper times of the two clocks will show different times, which are in general also different from $t$.

So there's no more paradoxical in this situation as in standard Euclidean geometry two curves connecting the same two points have in general different lengths.

"Resolving the paradox" does not only require confirming one of the calculations, it requires showing why the other proposed "solution" that gives a contradictory answer is wrong. You need to explain why the traveling twin will not calculate that his brother on Earth is younger.

 

[vanhees71]

Which "other proposed solution"? The proper times are completely independent of any choice of reference frame (and, of course, also of the choice of world-line parametrization), i.e., there is no doubt which twin is older after both's travels, no matter within which reference frame you calculate their proper times.

 

[FactChecker]

The traveling twin can not use the same simple calculation to determine the stationary brother's age. The traveling twin does not remain in a single inertial reference frame. He undergoes acceleration. An accurate calculation is more complicated. It gives the same answer as the stationary twin gets. From both points of view, the traveling twin is younger.

 

[vanhees71]

That doesn't matter. He can use an arbitrary (accelerating) rest frame. Then of course he has to use the adequate components of the fundamental form, $g_{\mu \nu}$.

 

[FactChecker]

That doesn't matter. He can use an arbitrary (accelerating) rest frame. Then of course he has to use the adequate components of the fundamental form, $g_{\mu \nu}$.

Yes, he can do a correct calculation. But that is not the "Twins Paradox". The Twins Paradox proposes that the traveling twin assumes that he is stationary and uses the exact same calculation method as the Earth twin, thereby calculating that the Earth twin is younger.

 

[vanhees71]

That's a wrong assumption, leading indeed to a paradox. What each twin has to calculate are the proper times it takes to travel, and these quantities are unique, i.e., independent of the coordinates and reference frames used to describe the twins' motion. You can thus simply calculate this quantity within an arbitrary inertial reference frame ("the computational frame"). There is no paradox, just a physical assumption that an ideal clock always shows its proper time, no matter of its motion relative to any inertial reference frame. This assumption has been verfied in various ways, among them with instable particles/nuclei in pretty high accelerations in storage rings.

 

[FactChecker]

That's a wrong assumption, leading indeed to a paradox.

Exactly. The "paradox" is false. IMO, the "solution" to the "paradox" is to explain what the error is and why. As far as calculating the correct answer, that is simple.

 

[PeroK]

Yes, he can do a correct calculation. But that is not the "Twins Paradox". The Twins Paradox proposes that the traveling twin assumes that he is stationary and uses the exact same calculation method as the Earth twin, thereby calculating that the Earth twin is younger.

The reason that is wrong is simple. The travelling twin is not at rest in a single inertial reference frame. A satisfactory calculation can be done using only inertial reference frames - or, by considering the invariance of proper time (length of the spacetime interval) using in general any coordinate system. The latter, however, requires more sophisticated mathematics.

Note that the asymmetry in the twin's journeys is manifest by considering the defined turnaround point in the original frame. The apparent symmetry requires that this be overlooked.

 

[Vanadium 50]

I never understood why one thinks that it helps to invent ever more complicated scenarios

This,

Problems seldom arise because the system under consideration is just not complicated enough.

 

[PeterDonis]

This is a response to a recent insight article regarding the twin paradox.

Do you mean this article?

https://www.physicsforums.com/insights/when-discussing-the-twin-paradox-read-this-first/

If so, your "response" is an unnecessarily long-winded attempt to describe the "spacetime geometry" viewpoint described in that article. You are constructing the same triangle in spacetime that the standard scenario constructs (in the idealized limit of an instantaneous turnaround).

Unfortunately, your attempt obfuscates the actual spacetime geometry because it uses Euclidean geometry, whereas the geometry of spacetime is Minkowskian. The straightedge for making lines is all right, but the compass is wrong; for Minkowskian geometry it should be a tool that draws hyperbolas about a given center, not circles. For this particular scenario, you can get away with it because moving a term from one side of the equation to the other makes it look like the ordinary Pythagorean theorem. But this method will not generalize to other scenarios; whereas the "spacetime geometry" viewpoint described in the Insights article works for any scenario whatever, in full generality.

 

[FactChecker]

Note that the asymmetry in the twin's journeys is manifest by considering the defined turnaround point in the original frame. The apparent symmetry requires that this be overlooked.

Yes. IMO, the key mistake is to confuse acceleration with the second derivative of position. That makes people think that the situation of the two twins is completely symmetric when each twin is used as the center of their reference frame. They put on blinders to ignore the physical acceleration and imagine the mathematics to be completely symmetric.

 

[PeroK]

Yes. IMO, the key mistake is to confuse acceleration with the second derivative of position. That makes people think that the situation of the two twins is completely symmetric when each twin is used as the center of their reference frame. They put on blinders to ignore the physical acceleration and imagine the mathematics to be completely symmetric.

It has nothing to do with acceleration. The asymmetry is more fundamental. The turnaround times differ.

 

[PeroK]

It has nothing to do with acceleration. The asymmetry is more fundamental. The turnaround times differ.

To do the maths:

Twin A measures twin B to travel for 5 years and a distance of 3 light years, then turn round.

Twin B measures Twin A to travel for 3 years and a distance of 1.8 light years, then turn round.

These are not the same!

 

[FactChecker]

It has nothing to do with acceleration. The asymmetry is more fundamental. The turnaround times differ.

In a purely mathematical framework, the relative positions, relative velocities, and derivatives of relative velocities are completely symmetric. The real difference that invalidates one calculation is the acceleration.

 

[PeroK]

In a purely mathematical framework, the relative positions, velocities, and derivatives of velocities, are completely symmetric. The real difference that invalidates one calculation is the acceleration.

This is wrong.

 

[FactChecker]

This is wrong.

If velocity is relative, then so are the derivatives of those velocities.

 

[PeroK]

If velocity is relative, then so are the derivatives of those velocities.

The relative velocity is the same. The turnaround times and distances are, however, different:

To do the maths:

Twin A measures twin B to travel for 5 years and a distance of 3 light years, then turn round.

Twin B measures Twin A to travel for 3 years and a distance of 1.8 light years, then turn round.

These are not the same!

 

[FactChecker]

As long as both remain in their own inertial reference frame as they travel, they see the same thing about themself and about the other twin.

 

[PeroK]

As long as both remain in their own inertial reference frame as they travel, they see the same thing about themself and about the other twin.

And yet the asymmetry is apparent for those with the inclination to look for it!

 

[PeroK]

As long as both remain in their own inertial reference frame as they travel, they see the same thing about themself and about the other twin.

Here's another example of asymmetry.

A train is moving relative to a platform. Let's say in the platform frame the train is the same length as the platform as it passes by. In the train frame, however, the platform is shorter than the train.

Your analyses assumes that what is observed in one frame must be observed in the other. As there is only relative motion and no acceleration. In your analysis, therefore, the platform must be the same length as the train also in the train frame.

That is the "unexpected" asymmetry that has relevance to the twin paradox.

 

[FactChecker]

Here's another example of asymmetry.

A train is moving relative to a platform. Let's say in the platform frame the train is the same length as the platform as it passes by. In the train frame, however, the platform is shorter than the train.

Your analyses assumes that what is observed in one frame must be observed in the other.

I wouldn't call it my analysis, since I am trying to explain the flaw in the analysis of those who are confused by the Twins Paradox.

As there is only relative motion and no acceleration. In your analysis, therefore, the platform must be the same length as the train also in the train frame.

That is the "unexpected" asymmetry that has relevance to the twin paradox.

Yes.
As long as both twins remain in their own inertial reference frame, there is complete symmetry. If A thinks that B is aging slower, then B thinks that A is aging slower.
Question: What breaks the symmetry?
Answer: The traveling twin, B, does not remain in a single inertial reference frame.
Question: What distinguishes the inertial reference frame of A from the non-inertial reference frame of B?
Answer: Acceleration.

 

[PeroK]

I wouldn't call it my analysis, since I am trying to explain the flaw in the analysis of those who are confused by the Twins Paradox.

Yes.
As long as both twins remain in their own inertial reference frame, there is complete symmetry. If A thinks that B is aging slower, then B thinks that A is aging slower.
Question: What breaks the symmetry?
Answer: The traveling twin, B, does not remain in a single inertial reference frame.
Question: What distinguishes the inertial reference frame of A from the non-inertial reference frame of B?
Answer: Acceleration.

You haven't read any of my posts. That's disappointing.

You're wrong about acceleration being the only resolution to twin paradox.

 

[FactChecker]

You haven't read any of my posts. That's disappointing.

You're wrong about acceleration being the only resolution to twin paradox.

It only takes one reason to establish an error of the twin paradox. There may be others.
As far as how many ways there are to get the correct answer, there are often many ways to get a correct answer.

 

[ergospherical]

… the … derivatives of relative velocities are completely symmetric. …

derivatives with respect to what parameter…?

 

[FactChecker]

derivatives with respect to what parameter…?

Each reference frame takes derivatives of its own variables (position, velocity) wrt its own variables (time). If you see problems with this, keep in mind that I am only trying to express what I believe those who are confused by the Twins Paradox are thinking. I personally see no paradox.

 

[PeterDonis]

In a purely mathematical framework, the relative positions, relative velocities, and derivatives of relative velocities are completely symmetric.

No, they're not. If you would actually do the math instead of waving your hands, this would be obvious. Even just realizing that the "rest frame" of the traveling twin is not an inertial frame should be enough.

I wouldn't call it my analysis, since I am trying to explain the flaw in the analysis of those who are confused by the Twins Paradox.

Before trying, you should read the Insights article linked to in post #12.

 

[PeterDonis]

You're wrong about acceleration being the only resolution to twin paradox.

It only takes one reason to establish an error of the twin paradox. There may be others.
As far as how many ways there are to get the correct answer, there are often many ways to get a correct answer.

Again, please read the Insights article linked to in post #12.

 

[FactChecker]

No, they're not. If you would actually do the math instead of waving your hands, this would be obvious. Even just realizing that the "rest frame" of the traveling twin is not an inertial frame should be enough.

I have a Ph.D. in pure mathematics and I don't think that I am not "waving my hands". There is a big difference between derivatives of velocities in a non-inertial reference frame and physical accelerations. IMO, that is a major problem for people who are struggling with the twin paradox. I have read your article and do not think it adequately addresses that issue.
With that being said, I feel that I should leave this thread to others.

 

[PeterDonis]

I have a Ph.D. in pure mathematics

Your credentials do not automatically mean everything you post is correct. @PeroK correctly pointed out a claim of yours that was wrong, the same one I did. If you have a Ph.D. in math, you should have no trouble doing the required math to either see that @PeroK and I are right and retract your claim, or show us the math that proves your claim is correct.

There is a big difference between derivatives of velocities in a non-inertial reference frame and physical accelerations.

Yes, agreed. But I don't think that is an important confusion in the OP of this thread.

IMO, that is a major problem for people who are struggling with the twin paradox.

That's not the sense I have gotten from other PF threads on the topic. Do you have any particular examples in mind?

I have read your article and do not think it adequately addresses that issue.

The article only uses proper acceleration and doesn't even mention coordinate acceleration, that's true. That's because I don't think coordinate acceleration even plays any part at all in analyzing the scenario, whereas proper acceleration does play a role at least in the standard scenario since it is a physical observable that is asymmetric between the twins.

With that being said, I feel that I should leave this thread to others.

Not until you either retract your claim or back it up with math. Drive-bys are not appreciated here.

 

[PeroK]

To give another explicit example. Suppose an alien spaceshift explored our part of the galaxy. They approach Earth at $0.6c$ and proceed to Alpha Centauri. In the local reference frame this journey is about 4.4 light years and takes about 7 years. The Aliens know this and can calculate this. The onboard journey time, however, is about 5.5 years.

Note that there is an asymmetry between the reference frames, as we have a single spaceship and two fixed points in the local frame.

We can also assume that we have a space station orbiting Alpha Centauri and this knows the local Earth time (using the Einstein synchronization convention).

In any case when the Aliens pass the space station, they are not surprised that 7 years Earth time has passed. What they cannot do is imagine that the time dilation of the Earth clock implies that only about 4 years has passed in the local reference frame during the journey.

In learning SR, resolution of this scenario should precede tackling the full twin paradox, which essentially puts two of these Alien journeys back to back - with some sort of turnaround, potentially requiring an acceleration phase.

In this way, the full twin paradox is resolved. Moreover, the acceleration phase is seen to be not critical to the argument, but merely a physical constraint in the process of changing direction.

 

[vanhees71]

It has nothing to do with acceleration. The asymmetry is more fundamental. The turnaround times differ.

Let's try my simple way for the standard scenario. We use the inertial frame of the resting twin as "calcluational frame", because that's the most simple one to calculate invariant (!!!) quantities.

The worldline of the twin at rest, parametrized with the "coordinate time" (which is this twin's proper time of course) is simply
$$x_A=(t , 0), \quad t \in [0,T].$$
The world line of the traveling twin is
$$x_B=\begin{cases} (t,vt) & \text{for} \quad t \in [0,T/2], \\
(t, v(T-t))&\text{for} \quad t \in [T/2,T]. \end{cases}$$
Then you get
$$\tau_A=\int_0^T \mathrm{d} t \sqrt{\dot{x}_A(t) \cdot \dot{x}_A(t)}= T$$
and
$$\tau_B=\int_0^T \mathrm{d} t \sqrt{\dot{x}_B(t) \cdot \dot{x}_B(t)}=\int_0^T \mathrm{d} t \sqrt{1-v^2}=T \sqrt{1-v^2}.$$
Case closed.

 

[Peter Strohmayer]

You're wrong about acceleration being the only resolution to twin paradox.

The world line of the traveling twin is not straight. So how can one claim that acceleration is not relevant to understanding the "twin paradox"?

 

[vanhees71]

I'd say it rather has to do with time dilation than with acceleration. It's about the dependence of the time between two events on the clock that's used which measures them. All you can say is that the measured time is maximal for a clock moving along a geodesic in spacetime. In Minkowski spacetime that's uniform rectilinear motion.