Three Masses - pulley, rotational and translational forces

In summary, the system consists of a green hoop with mass 2.4 kg and radius 0.18 m, a blue solid disk pulley with mass 2.4 kg and radius 0.09 m, and an orange sphere on a flat horizontal surface with mass 3.3 kg and radius 0.25 m. The hoop is not rotating and will simply fall, while the pulley will rotate and accelerate in the same direction as the falling mass. The tension forces on either side of the pulley will be different. The sphere will also rotate and experience a force from friction due to rolling without slipping. The tension force acts through the center of the sphere, but there is also a force from friction at the
  • #1
iluvcanucksfo
3
0
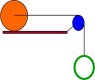
An green hoop with mass mh = 2.4 kg and radius Rh = 0.18 m hangs from a string that goes over a blue solid disk pulley with mass md = 2.4 kg and radius Rd = 0.09 m. The other end of the string is attached to a massless axel through the center of an orange sphere on a flat horizontal surface that rolls without slipping and has mass ms = 3.3 kg and radius Rs = 0.25 m. The system is released from rest.

1)What is magnitude of the linear acceleration of the hoop?

I'm wondering how to solve this question, especially wondering how the tension forces would be related to each other throughout the system?
 

Attachments

  • threemasses.png
    threemasses.png
    2.1 KB · Views: 870
Physics news on Phys.org
  • #2
From what is written, the hoop is not rotating - so it is just a mass falling: you can do the free body diagram for that one.

The pulley rotates, the net torque on the pulley will have it accelerate consistently with the acceleration of the falling mass. Label the tensions on each side of the pulley differently.

The sphere is rotating, the tension acts through the center, but there is a force from friction (rolling without slipping) where there is contact with the table. Just think of it as a wheel being pulled by the axle - you will have course notes for that situation.
 

FAQ: Three Masses - pulley, rotational and translational forces

What is a pulley and how does it affect the motion of three masses?

A pulley is a simple machine that consists of a wheel with a groove around its circumference, which is used to change the direction of a force applied to a rope or cable. In a system with three masses, the pulley can affect the motion by transferring forces between the masses through the tension in the rope.

How do rotational forces come into play in a system with three masses and a pulley?

Rotational forces, also known as torque, are generated when a force is applied to a lever arm, such as the pulley in this system. These forces can cause the masses to rotate around the pulley, changing the direction of their motion and affecting their overall velocity and acceleration.

How are translational forces involved in a system with three masses and a pulley?

Translational forces, also known as linear forces, are forces that act in a straight line and can cause a body to move in a specific direction. In a system with three masses, translational forces are present in the form of the weight of each mass and the tension in the rope connecting them.

How can the forces on each mass be calculated in a system with three masses and a pulley?

The forces on each mass can be calculated using Newton's Second Law of Motion, which states that the net force on an object is equal to its mass multiplied by its acceleration. By considering the forces acting on each mass, including the weight and tension forces, their accelerations can be determined and the net force can be calculated.

How does the concept of conservation of energy apply to a system with three masses and a pulley?

The concept of conservation of energy states that energy cannot be created or destroyed, only transferred or converted from one form to another. In a system with three masses and a pulley, the total energy of the system, which includes gravitational potential energy and kinetic energy, remains constant as the masses move and interact with each other.

Similar threads

I Translational force of a pulley
Replies
27
Views
2K
I Pulley question -- Three pulleys lifting a mass...
Replies
2
Views
955
Wheel moving in rotation and translation
Replies
15
Views
2K
1 pulley with mass, 1 mass on the cord, 1 external force, no gravity
Replies
16
Views
2K
What mass must be placed on the cord to keep the pulley from rotating?
Replies
1
Views
403
Will a Massless Pulley with Friction Rotate with Unequal Masses on Either Side?
Replies
1
Views
1K
Rigid Body Rotational or Translational ?
Replies
10
Views
2K
I Lift Force of a Rotating Sphere in the Air
Replies
7
Views
2K
Understanding Accelerating Pulley Systems: Tension, Forces, and Analysis
Replies
5
Views
2K
Why does adding more pulleys increase the force on a block?
Replies
21
Views
4K

Hot Threads

Recent Insights

Back
Top