- #1
Frank-95
- 52
- 1
Hello. I have a doubt regarding the following problem:
1. Homework Statement
Calculate capacitors' capacity to rephase (cos(φF) = 1) the load ZL
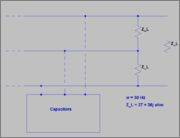
The formula to calculate capacity in this case is:
CY = P(tan(φi) - tan(φF))/ωVrms2
or
CΔ = P(tan(φi) - tan(φF))/3ωVrms2
Firstly I converted the delta load in a star load:
ZLY = ZLΔ / 3 = 9 + 12 j Ω = 15e53,13j
The load phase is then 53,13. The final phase must be cos(φF) = 1 -> φF = 0.
In the image I posted I made an error: the pulsation isn't 50 Hz, the frequency is; hence pulsation ω = 100 π Hz.
Now I have initial and final phase, pulsation and I should apply the formula for finding capacitor, but the problem voluntarly do not give source voltages, so my doubt is: should I leave capacity dependent from power and root mean square voltage, or am I not considering something and I can make some more calculation? Thanks :)
1. Homework Statement
Calculate capacitors' capacity to rephase (cos(φF) = 1) the load ZL
Homework Equations
The formula to calculate capacity in this case is:
CY = P(tan(φi) - tan(φF))/ωVrms2
or
CΔ = P(tan(φi) - tan(φF))/3ωVrms2
The Attempt at a Solution
Firstly I converted the delta load in a star load:
ZLY = ZLΔ / 3 = 9 + 12 j Ω = 15e53,13j
The load phase is then 53,13. The final phase must be cos(φF) = 1 -> φF = 0.
In the image I posted I made an error: the pulsation isn't 50 Hz, the frequency is; hence pulsation ω = 100 π Hz.
Now I have initial and final phase, pulsation and I should apply the formula for finding capacitor, but the problem voluntarly do not give source voltages, so my doubt is: should I leave capacity dependent from power and root mean square voltage, or am I not considering something and I can make some more calculation? Thanks :)