Reinhardt Walzer
- 7
- 0
Been studying Special Relativity in Uni. and I've noticed that all examples of relativistic motion provided are motions only along a single axis, like the one below:
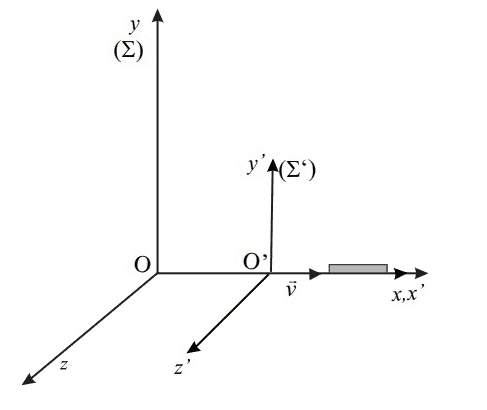
The particle's Reference Frame is moving only along the X axis in the example above.
In this case the Lorentz Transformation for Time is this: ##t^{'}=\gamma(t-\frac{vx}{c^{2}})##.
But what about the case shown below:
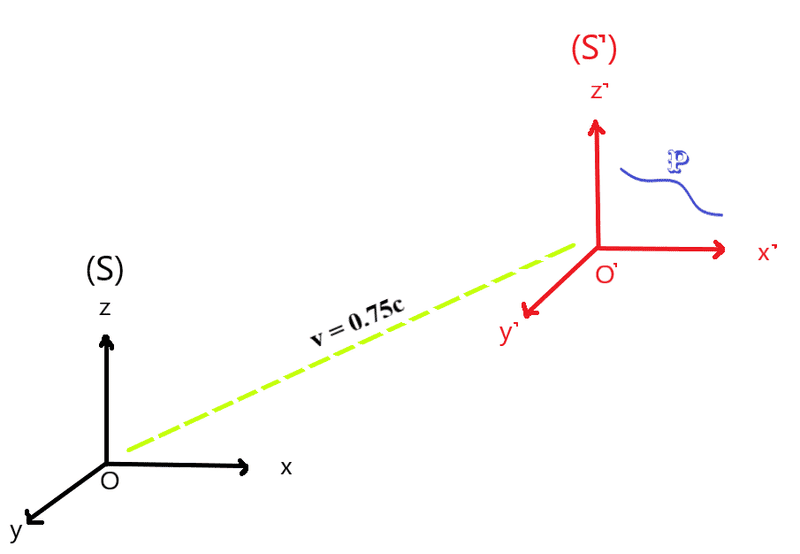
How would I write the Lorentz Transformation for Time in this case?
The particle's Reference Frame is moving only along the X axis in the example above.
In this case the Lorentz Transformation for Time is this: ##t^{'}=\gamma(t-\frac{vx}{c^{2}})##.
But what about the case shown below:
How would I write the Lorentz Transformation for Time in this case?
- Like this: ##t^{'}=\gamma(t-\frac{\vec v \cdot \vec r}{c^{2}})## How would ##\vec v \cdot \vec r## even look like?
- Or would I need to have three different components of time for each axis: ##t^{'}_{x}=\gamma(t-\frac{v_{x}x}{c^{2}})## ; ##t^{'}_{y}=\gamma(t-\frac{v_{y}y}{c^{2}})## ; ##t^{'}_{z}=\gamma(t-\frac{v_{z}z}{c^{2}})##