- #36
Grimble
- 485
- 11
but surely x - the distance the clock has travelled, OD, = vtIbix said:But the Lorentz transforms tell us that T′=γ(t−vx/c2)
then
T'=γt(1-v2/c2) = t/γ
. The distance OT' is the distance, if the traveling clock were a light clock, that light would have traveled from the initial event O to the red turnaround at time T' in the stay-at-home frame.Ibix said:in the frame of the stay-at-home:
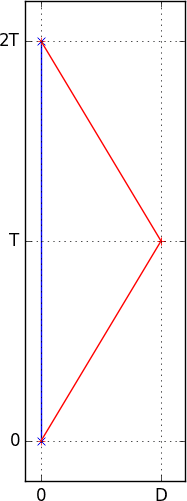
... and T' occurs at time T on the time axis on the stay-at-home clock's frame
One cannot get much more basic than time and distance axes, T and X at 90°.
I am sorry but I am just having difficulty following what is wrong with the most simple and basic mathematical principles - or maybe I am just being naïve... ?