Time-Discrete Odometry: Solving Complicated Equations By Hand

[RandomUserName]

Hello, I have another question regarding my cognitive robotics class. Here is my current task:
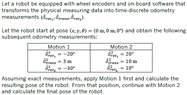
View attachment 6205
And this is the slide from the lecture about this topic:
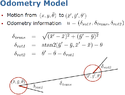
View attachment 6206
Now just plugging in everything I know into the formulas, I get this:
\(\displaystyle \boxed{3 = \sqrt{x'^{2} + y'^{2}}\\
-20 = atan2(y',x')\\
-30 = \theta' - 20}\\
\boxed{y' = \sqrt{9-x'^{2}}\\
-20 = atan2(\sqrt{9-x'^{2}},x')\\
\theta' = -10}\\
\boxed{y \approx 1.026\\
x = 3 \cos(20) \approx 2.819\\
\theta' = -10}\)

But then, when I try to perform the second motion, I get the following:
\(\displaystyle \boxed{10 \approx \sqrt{(x' - 2.189)^{2} + (y' - 1.026)^{2}}\\
20 \approx atan2(y' - 1.026, x' - 2.819) + 10\\
10 = \theta' + 10 - 20}\)
which is just way too complicated for me to solve (and we are supposed to solve this by hand).

Am I doing this right at all? Or is there some other formula that I should use? I haven't been able to find anything that helps me using Google :(

 

[I like Serena]

Re: time-discrete odometry

Now just plugging in everything I know into the formulas, I get this:
\(\displaystyle \boxed{3 = \sqrt{x'^{2} + y'^{2}}\\
-20 = atan2(y',x')\\
-30 = \theta' - 20}\)

Hi again RandomUserName! (Smile)

Let's take a look at this first step.
First off, shouldn't it be $-30 = \theta' - -20 = \theta' + 20$? (Wondering)

Okay, now for an intermezzo about polar coordinates.
Suppose we have the following right triangle:
\begin{tikzpicture}[ultra thick, font=\Large, blue]
\draw[thin] (4,0) rectangle +(-0.3,+0.3);
\draw (0,0) -- node[below] {$x$} (4,0) -- node

{$y$} (4,3) -- node[above left] {$r$} cycle;
\node[above right, xshift=4mm] (0,0) {$\alpha$};
\end{tikzpicture}
Then we have:
$$r=\sqrt{x^2+y^2}\\ \alpha = \operatorname{atan2}(y,x) \\ x=r\cos\alpha \\ y=r\sin\alpha$$

Can we find $x$ and $y$ from $r$ and $\alpha$ in the problem at hand? (Wondering)​

 

[RandomUserName]

Re: time-discrete odometry

Hi again RandomUserName! (Smile)

Let's take a look at this first step.
First off, shouldn't it be $-30 = \theta' - -20 = \theta' + 20$? (Wondering)

Yes, you are correct, I messed up the sign there => \(\displaystyle \theta' = -50°\)

Okay, now for an intermezzo about polar coordinates.
Suppose we have the following right triangle:
\begin{tikzpicture}[ultra thick, font=\Large, blue]
\draw[thin] (4,0) rectangle +(-0.3,+0.3);
\draw (0,0) -- node[below] {$x$} (4,0) -- node

{$y$} (4,3) -- node[above left] {$r$} cycle;
\node[above right, xshift=4mm] (0,0) {$\alpha$};
\end{tikzpicture}
Then we have:
$$r=\sqrt{x^2+y^2}\\ \alpha = \operatorname{atan2}(y,x) \\ x=r\cos\alpha \\ y=r\sin\alpha$$

Can we find $x$ and $y$ from $r$ and $\alpha$ in the problem at hand? (Wondering)​

Omg, the more complicated the task gets, the more simple stuff I seem to not think of :D

edit:
Ok, I figured out my mistake, was another sign error... But now I'm good. Thank you again!​