Tipping a crate friction physics problem

[dharcha1]

A worker wants to turn over a uniform 1010 N rectangular crate by pulling at 53.0 degrees on one of its vertical sides. The floor is rough enough to prevent the crate from slipping.

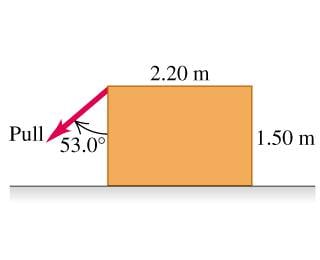
1. What pull is needed to just start the crate to tip?
2. How hard does the floor push on the crate?
3. Find the friction force on the crate.
4. What is the minimum coefficient of static friction needed to prevent the crate from slipping on the floor?

1. torque = (F_pull)cos(270-53)(1.5m) = 1010 * 1.5 = 1515 N
the problem is getting started. i don't think i did this right.

 

[rl.bhat]

. torque = (F_pull)cos(270-53)(1.5m) = 1010 * 1.5 = 1515 N
This is the counterclockwise torque. What is the clockwise torque?

 

[nlightner]

1. To just start the crate to tip, the worker would need to apply a torque of at least 1515 N*m. This can be calculated by using the formula torque = force * distance, where the force is the pull applied by the worker and the distance is the length of the vertical side of the crate.

2. The floor will push back on the crate with an equal and opposite force to the pull applied by the worker. This is known as Newton's Third Law of Motion, which states that for every action, there is an equal and opposite reaction. Therefore, the floor will push on the crate with a force of 1515 N in the opposite direction to the pull applied by the worker.

3. The friction force on the crate can be calculated by using the formula F_friction = μ * N, where μ is the coefficient of friction and N is the normal force. In this case, the normal force is equal to the weight of the crate, which is 1010 N. Therefore, the friction force can be calculated as F_friction = μ * 1010 N. However, since we are looking for the minimum coefficient of static friction, we can set the friction force equal to the maximum possible force, which is the force applied by the worker (1515 N). Therefore, we can rearrange the equation to find the minimum coefficient of static friction as μ = F_friction / N = 1515 N / 1010 N = 1.5.

4. The minimum coefficient of static friction needed to prevent the crate from slipping on the floor is 1.5. This means that the coefficient of static friction between the crate and the floor must be at least 1.5 for the crate to remain in place when the worker pulls on it at an angle of 53 degrees. If the coefficient of static friction is less than 1.5, the crate will start to slip and the worker will need to apply a greater force to keep it from tipping.