To construct the Koch snowflake curve

[Chris L T521]

Thanks again to those who participated in last week's POTW! Here's this week's problem!

-----

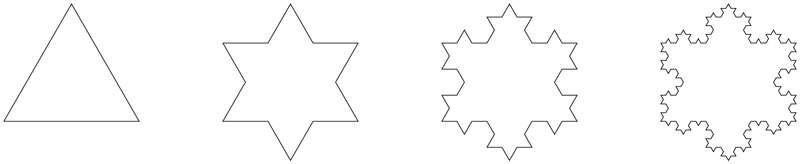
Problem: To construct the Koch snowflake curve, start with an equilateral triangle with sides of length 1. Step 1 in the construction is to divide each side into three equal parts, construct an equilateral triangle on the middle part, and then delete the middle part (see the figure below). Step 2 is to repeat Step 1 for each side of the resulting polygon. This process is repeated at each succeeding step. The Koch snowflake curve is the curve that results from repeating this process indefinitely.

Figure: The $n=0$, $n=1$, $n=2$ and $n=3$ approximating curves for the Koch snowflake.​

(a) Let $s_n$, $\ell_n$ and $p_n$ represent the number of sides, the length of a side, and the total length of the $n$th approximating curve (the curve obtained after Step $n$ of the construction), respectively. Find formulas for $s_n$, $\ell_n$ and $p_n$.

(b) Show that $p_n\to\infty$ as $n\to\infty$.

(c) Sum an infinite series to find the area enclosed by the Koch snowflake curve.

(Parts (b) and (c) show that the Koch snowflake curve is indefinitely long but encloses only a finite area.)

-----

 

[Chris L T521]

This week's problem was correctly answered by MarkFL. You can find his solution below.

[sp](a) The number of sides:

We see that as defined, each iteration divides all of the sides from the previous iteration into 4 smaller sides. This leads to the linear difference equation:

$$s_{n+1}=4s_{n}$$ where $$s_{0}=3$$

The characteristic root is $r=4$ and so the closed-form is:

$$s_{n}=c_14^n$$

Using the initial condition, we may determine the parameter $c_1$:

$$s_{0}=c_14^0=c_1=3$$

And so we find:

$$s_{n}=3\cdot4^n$$

The length of a side:

We see that as defined, each iteration as given in step 1 of the construction is to divide each side into 3 equal parts, hence the sides are 1/3 the length of the previous iteration. This leads to the difference equation:

$$\ell_{n+1}=\frac{1}{3}\ell_{n}$$ where $$\ell_{0}=1$$

The characteristic root is $$r=\frac{1}{3}$$ and so the closed-form is:

$$\ell_{n}=c_13^{-n}$$

Using the initial condition, we may determine the parameter $c_1$:

$$\ell_{0}=c_13^{-0}=c_1=1$$

And so we find:

$$\ell_{n}=3^{-n}$$

The total perimeter:

To find the perimeter, we need only take the product of the number of sides and the length of each side, hence:

$$p_n=s_n\cdot\ell_n=\frac{4^n}{3^{n-1}}$$

(b) The perimeter at infinity:

$$L=\lim_{n\to\infty}p_n=\lim_{n\to\infty}\frac{4^n}{3^{n-1}}$$

$$\frac{L}{3}=\lim_{n\to\infty}\left(\frac{4}{3} \right)^n$$

Taking the natural log of both sides, we obtain:

$$\ln\left(\frac{L}{3} \right)=\lim_{n\to\infty}n\ln\left(\frac{4}{3} \right)=\ln\left(\frac{4}{3} \right)\lim_{n\to\infty}n=\infty$$

Converting from logarithmic to exponential form, we find:

$$L=3e^{\infty}=\infty$$

Thus, we conclude that the perimeter grows without bound as the fractal is iterated to infinity.

(c) The area at infinity:

Let $A_{n}$ represent the area of the $n$th curve. To get $A_{n+1}$ we must add the area of $s_{n}$ equilateral triangles whose side lengths are $\ell_{n+1}$. That is:

$$A_{n+1}=A_{n}+s_{n}\left(\frac{\sqrt{3}}{4}\ell_{n+1}^2 \right)$$

$$A_{n+1}=A_{n}+3\cdot4^n\left(\frac{\sqrt{3}}{4} \left(3^{-(n+1)} \right)^2 \right)$$

$$A_{n+1}=A_{n}+3^{-\left(2n+\frac{1}{2} \right)}\cdot4^{n-1}$$ where $$A_{0}=\frac{\sqrt{3}}{4}$$

Thus, the total area of the snowflake after $n$ iterations is:

$$A_{n}=\frac{\sqrt{3}}{4}+\frac{3\sqrt{3}}{16}\sum_{k=1}^{n}\left(\frac{4}{9} \right)^k$$

Let:

$$S_n=\sum_{k=1}^{n}\left(\frac{4}{9} \right)^k$$

$$\frac{4}{9}S_n=\sum_{k=1}^{n}\left(\frac{4}{9} \right)^{k+1}=S_n-\frac{4}{9}+\left(\frac{4}{9} \right)^{n+1}$$

$$\frac{5}{9}S_n=\frac{4}{9}-\left(\frac{4}{9} \right)^{n+1}$$

$$S_n=\frac{4}{5}-\frac{9}{5}\left(\frac{4}{9} \right)^{n+1}=\frac{4}{5}\left(1-\left(\frac{4}{9} \right)^n \right)$$

Thus, we obtain:

$$A_{n}=\frac{\sqrt{3}}{4}\left(1+\frac{3}{5}\left(1-\left(\frac{4}{9} \right)^n \right) \right)=\frac{\sqrt{3}}{20}\left(8-\left(\frac{4}{9} \right)^n \right)$$

And as a consequence, we find:

$$A_{\infty}=\lim_{n\to\infty}A_n=\frac{\sqrt{3}}{20}\left(8-0 \right)=\frac{2\sqrt{3}}{5}$$

Thus, we have shown that the Koch snowflake is an infinitely long curve enclosing a finite area.[/sp]