To find the center of gravity of a particular quadrilateral

[gnits]

Homework Statement

To find the center of gravity of a quadrilateral

Relevant Equations

Moments

Could I please ask for help with the following question. Part 2 is my problem. I have no idea how to begin, any hints would be much appreciated:

1) Prove that the center of gravity of a uniform triangular lamina is the same as that of three equal particles placed at the vertices of the lamina

I'm ok here, done that.

2) A uniform lamina of weight W is in the shape of a quadrilateral ABCD. The diagonals AC, BC meet at P, where AP < PC, BP < PD and Q, R are points on AC, BD respectively such that QC = AP, RD = BP. By replacing the triangles ABD, BCD by equivalent systems of particles, or otherwise, prove that the center of gravity of the lamina is the same as that of a particle of weight W/3 at Q and a particle of weight 2W/3 at the midpoint of BD.

Here is a diagram:

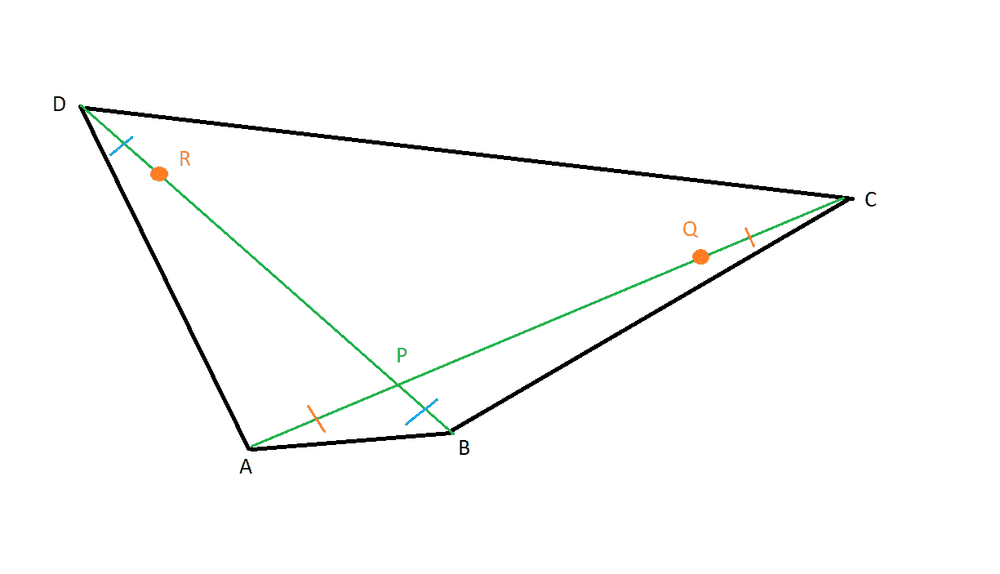
(The blue and orange strokes are meant to show the equality of the lengths of the segments that they are on)

I don't mind which way it is proved, by equivalent particle systems or "otherwise".

I started by setting up cartesian coordinates at A, but I don't think that helps.

Thanks for any help,
Mitch,

 

[Lnewqban]

You could find the CG of two or four triangles using the method in #1; then, you could find the point of balance of those CG’s by using summation of moments.
It seems that the problem does not give specific location for point Q; perhaps I am missing something that is evident,...as usual.

 

[onatirec]

It seems that the problem does not give specific location for point Q

QC = AP

 

[gnits]

You could find the CG of two or four triangles using the method in #1; then, you could find the point of balance of those CG’s by using summation of moments.
It seems that the problem does not give specific location for point Q; perhaps I am missing something that is evident,...as usual.

Yes, this is what I first started to do but then I couldn't see how to assign the weights. Let's take triangle ABD. I want to put three equal weights at each vertex, each weight should be 1/3 of the weight of triangle ABD. But what is the weight of triangle ABD in terms of W ? I only know that the weight of triangle ABD + weight of triangle BCD = W.

 

[Lnewqban]

Because the thickness and material of the quadrilateral is homogeneous, its CG is located at its centroid.
Please, see:
https://en.m.wikipedia.org/wiki/Centroid

https://www.engineeringtoolbox.com/center-gravity-d_1310.html

If you can calculate the location of the centroid of each triangle; then, the summation of the triangle areas x centroid distances about the total CG should be equal to zero.

 

[gnits]

So I could proceed be setting up Cartesian axes at A(0,0), B(Bx, By), C(Cx, Cy) and D(Dx, Dy). then the centroid of triangle ABD would be ( (Bx + Dx) / 3 , (By + Dy) / 3 ) and that of BCD would be ( (Bx + Cx + Dx) / 3 , (By + Cy + Dy) / 3 ). Triangle areas could be calculated in terms of these coordinates and then multiplied by distances of these centroids from centroid of quadrilateral and equated to zero. Am I missing a more elegant way?

 

[haruspex]

Looks to me that one has to consider various different triangles and take sums and differences. The target relationship gives some clues.

 

[Lnewqban]

There should be a point (let's call it E) located between D and C, which forms a triangle with B and C, which area is 1/3 of the total area.
The centroid of that triangle is located at Q.

The ABED quadrilateral has 2/3 of the total area, or twice the area of triangle BCE.
The centroid of that quadrilateral is located at midpoint of diagonal BD (let's call it F).

The CG of the total area is located on the line joining Q and F, at a distance of 1/3 QF from point F and 2/3 QF from point Q.

 

[haruspex]

It helps to define a convenient notation. E.g. we could write a sum of terms as masses times points (as vectors).
The masses of triangles ABC, ADC are in the ratio BP:PD. Write x for BP/BD.
If M is the centroid of the quadrilateral:
$WM=\frac W3x(A+B+C)+\frac W3(1-x)(A+D+C)$
$=\frac W3(A+C+D+x(B-D))=\frac W3(P+Q+D+x(B-D))$

There is a simple relationship between x and the vectors P, B and D.
Combining these leads to the answer.

 

[gnits]

It helps to define a convenient notation. E.g. we could write a sum of terms as masses times points (as vectors).
The masses of triangles ABC, ADC are in the ratio BP:PD. Write x for BP/BD.
If M is the centroid of the quadrilateral:
$WM=\frac W3x(A+B+C)+\frac W3(1-x)(A+D+C)$
$=\frac W3(A+C+D+x(B-D))=\frac W3(P+Q+D+x(B-D))$

There is a simple relationship between x and the vectors P, B and D.
Combining these leads to the answer.

Thanks you very much indeed. I wouldn't have seen this way of approaching it. I've definitely learned from your help and also been able to complete the question.

 

[gnits]

There should be a point (let's call it E) located between D and C, which forms a triangle with B and C, which area is 1/3 of the total area.
The centroid of that triangle is located at Q.

The ABED quadrilateral has 2/3 of the total area, or twice the area of triangle BCE.
The centroid of that quadrilateral is located at midpoint of diagonal BD (let's call it F).

The CG of the total area is located on the line joining Q and F, at a distance of 1/3 QF from point F and 2/3 QF from point Q.

Thanks very much for your help. I am interested in this method but I can't follow it fully. Indeed I can see that there must be a point (say E) on CD that forms a triangle with BC which is 1/3 of the total area of the trapezium. I don't see though how this implies that the centroid of that triangle should be at Q. Thanks for any clarification.

 

[Lnewqban]

Thanks very much for your help. I am interested in this method but I can't follow it fully. Indeed I can see that there must be a point (say E) on CD that forms a triangle with BC which is 1/3 of the total area of the trapezium. I don't see though how this implies that the centroid of that triangle should be at Q. Thanks for any clarification.

I don't see it clearly enough to be helpful; but just wanted to share some of my views of the problem.

The shape and proportions of the shown figure may not be at scale, but I believe that the statement "... and a particle of weight 2W/3 at the midpoint of BD." implies that BD is a common side with a triangle of same area and proportions than triangle ABD, which should be a reflection of it.

That triangle could be BED, having an area of 1/3 W itself and the location of its CG mirroring the location of the CG of triangle ABD respect to common side BD.
I would like to see your final response to the problem, if you don't mind.
Thank you.

 

[gnits]

I don't see it clearly enough to be helpful; but just wanted to share some of my views of the problem.

The shape and proportions of the shown figure may not be at scale, but I believe that the statement "... and a particle of weight 2W/3 at the midpoint of BD." implies that BD is a common side with a triangle of same area and proportions than triangle ABD, which should be a reflection of it.

That triangle could be BED, having an area of 1/3 W itself and the location of its CG mirroring the location of the CG of triangle ABD respect to common side BD.
I would like to see your final response to the problem, if you don't mind.
Thank you.

I followed haruspex up to his last equation. From there we know that BP = P - B and BD = D - B and so as x = BP / BD then x = (P - B) / (D - B) so we substitute this into haruspex's last equation and the (B - D) terms cancel, as do the P terms. We are left with WM = (W/3)*(Q + D + B) = (W/3)Q + (W/3)D + (W/3)B which is clearly equivalent to a weight of W/3 at Q and 2W/3 at the midpoint of BD.

Thanks again for your help.