To find the magnitude of the resultant of forces around a triangle

[gnits]

Homework Statement

To find the magnitude of the resultant of forces around a triangle

Relevant Equations

Resolving forces and calculating moments

Could I please ask for advice with the following:

ABC is a right-angled triangle in which AB = 4a; BC = 3a. Forces of magnitudes P, Q and R act along the directed sides AB, BC and CA respectively.

a) Find the ratios P:Q:R if their resultant is a couple.
b) If the force along the directed line AC is now reversed, find in terms of P the magnitude of the resultant of the new system.

Part a) is done (with the help of others on this forum) but I'm stuck on part b)

Book abswer is: 35P/12

Here's my working:

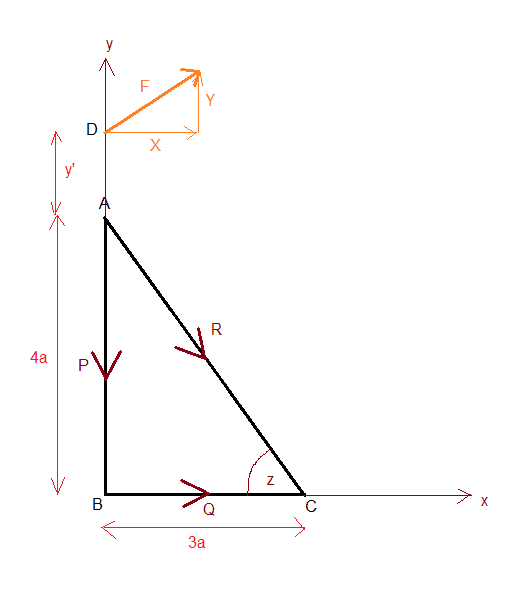
In the diagram F is the resultant. I assume it's line of action to pass through (0, 4a + y').

Hypotenuse = 5a

cos(z) = 3/5
sin(z) = 4/5

Resolving horizontally:
Q + 3R/5 = X

Resolving vertically:
P + 4R/5 + Y

So I need to calculate sqrt(X^2 + Y^2) in terms of P only, so ideally I would replace R and Q with equivalents in terms of P.

Taking moments about A:
4aQ=-Xy'

Taking moments about B:
-3R/5*4a = -X(4a+y')

which gives:

12Ra/5 = X(4a+y')

Taking moments about C:

3aP=-X(4a+y')

EDIT. I see that my moments about C are wrong, I failed to take into account the moment of Y about this point. Am continuing to work on this. Should be 3aP = -X(4a+y') - 3aY. Still leads me to R = -5P/4

These last two lead to R = -15P/12 = -5P/4

So I have R in terms of P but I still need Q in terms of P and this I can't see how to do. I tried moments about D but all derived relationships lead me to 0 = 0.

Thanks for any help.

 

[haruspex]

You don't seem to be using the ratios of the forces you found in the first part.
I don't think taking moments in the second part will be helpful.

 

[gnits]

But aren't those ratios predicated on the assumption that the resultant is a couple? The phrasing of the second part doesn't suggest to me that I can assume a resultant couple now that the force along AC has been reversed.

EDIT: Ok I see that the result about the ratio of P, Q, and R is indeed still valid as R still has the same magnitude because it has only had it's direction reversed.

So I still have P/Q = 4/3 and Q/R = 3/5
(because the answer to part a) is that P : Q : R = 4 : 3 : 5)

Proceeding as before:

Resolving horizontally:
Q + 3R/5 = X

Resolving vertically:
P + 4R/5 + Y

But now I know that Q = 3P/4 and R = 5Q/3 and so R = 5P/4

This gives 3P/4 + 3P/4 = X and so X = 3P/2

and P + P = Y and so Y = 2P

and so magnitude of resultant = sqrt(X^2 + Y^2) = sqrt(9P^2/4 + 4P^2) = sqrt(9P^2/4 + 16P^2/4) = 5P/2

Which is not equal to book answer of 35P/12

Thanks for any verification,
Mitch.

 

[haruspex]

But aren't those ratios predicated on the assumption that the resultant is a couple? The phrasing of the second part doesn't suggest to me that I can assume a resultant couple now that the force along AC has been reversed.

EDIT: Ok I see that the result about the ratio of P, Q, and R is indeed still valid as R still has the same magnitude because it has only had it's direction reversed.

So I still have P/Q = 4/3 and Q/R = 3/5
(because the answer to part a) is that P : Q : R = 4 : 3 : 5)

Proceeding as before:

Resolving horizontally:
Q + 3R/5 = X

Resolving vertically:
P + 4R/5 + Y

But now I know that Q = 3P/4 and R = 5Q/3 and so R = 5P/4

This gives 3P/4 + 3P/4 = X and so X = 3P/2

and P + P = Y and so Y = 2P

and so magnitude of resultant = sqrt(X^2 + Y^2) = sqrt(9P^2/4 + 4P^2) = sqrt(9P^2/4 + 16P^2/4) = 5P/2

Which is not equal to book answer of 35P/12

Thanks for any verification,
Mitch.

There is a slightly easier way. Since the net force was zero, reversing R must lead to a net force of 2R=5P/2.
I have no idea where 35P/12 could come from.

 

[gnits]

There is a slightly easier way. Since the net force was zero, reversing R must lead to a net force of 2R=5P/2.
I have no idea where 35P/12 could come from.

Thanks very much for your reply and confirmation of the answer,

Mitch.