To find the modulus of elasticity of a light elastic string

[gnits]

Homework Statement

To find the modulus of elasticity of a light elastic string

Relevant Equations

Moments

Could I please ask for help with the following question?

Four uniform rods of equal length l and weight w are freely jointed to form a framework ABCD. The joints A and C are connected by a light elastic string of natural length a. The framework is freely suspended from A and takes up the shape of a square. Find the modulus of elasticity of the string.

Formula for modulus of elasticity is M = T * a/x where T is the tension in the string, a the natural length and x the extension.

Here's my diagram:

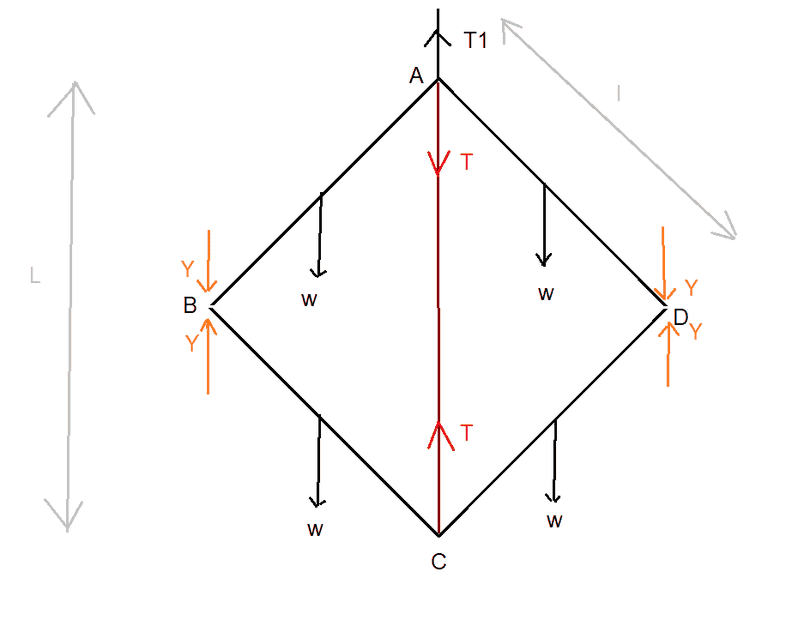
The book answer is M = 2aw / ( sqrt(2) * l - a)

I have shown from the diagram above that the extension of the string is sqrt(2) * l - a

So what remains is for me to show that the tension in the string is 2w.

I've split the diagram in half and shown the internal reactions in the hinges at B and D and by considering section BC alone and taking moments about C have shown that Y = w/2

But I'm not seeing a way to find T = 2W. I suspect my force labelling may be wrong?

Thanks,
Mitch.

 

[Chestermiller]

Try a moment balance for rod AD about joint D.

Incidentally, the equation for the modulus of elasticity is incorrect. Just consider the case where the string is in stretched, with a=x.

 

[gnits]

Thanks for the reply. From my diagram if I take moments of rod AD about D I get:

T1 * l/sqrt(2) - T * l/sqrt(2) - w * (l/2)*(1/sqrt(2)) = 0

Can divide both sides by l/sqrt(2) to give:

T1 - T - w/2 = 0

Resolving vertically for the whole system I have that T1 = 4w and so the equation above becomes:

T = 4w - w/2 leads to T = 7w/2

Not what I had expected. What is my mistake?

Concerning the formula, I am using the following from the textbook I am working with

Thanks again,
Mitch.

 

[TSny]

From my diagram if I take moments of rod AD about D I get:

T1 * l/sqrt(2) - T * l/sqrt(2) - w * (l/2)*(1/sqrt(2)) = 0

You have not accounted for all of the forces that act on rod AD. For example, at point A, rod AC can exert a force on rod AD.

Also, to maintain symmetry in the problem, I would assume that the supporting force $T_1$ is split such that $\large \frac{T_1}{2}$ acts at point A on rod AB and $\large \frac{T_1}{2}$ acts at point A on rod AD. Likewise, the elastic force $T$ can be assumed to split equally between rods AB and AD at point A and equally between rods BC and CD at point C.

-------------------------------------------------------
If you are familiar with the principle of virtual work then you can deduce the elastic tension $T$ fairly quickly without setting up any torque equations or drawing any free-body diagrams for the individual rods.

However, please don't let this post hijack your discussion with @Chestermiller

 

[gnits]

Thanks very much indeed Chestermiller and TSny for your help. Very much appreciated. It has enabled me complete the question.

 

[Chestermiller]

Thanks very much indeed Chestermiller and TSny for your help. Very much appreciated. It has enabled me complete the question.

That's good because I'm still struggling with this deceptively simple problem.

 

[Chestermiller]

I finally solved this, rather inelegantly, by doing force balances on an upper and a lower strut in both the normal and the axial directions to a strut, to get the reaction forces on the ends of the struts. This showed that the vertical component of force exerted by each strut on the right- and left-side connectors is zero. This simplified the vertical force balances on the upper and lower halves of the assembly.

 

[TSny]

The principle of virtual work provides a nice way to determine the tension $T$ in the elastic cord.

The principle states that if a system is in equilibrium and you imagine any virtual, small displacement of the system which is consistent with any constraints, then the net work done by the external forces equals zero.

The figure on the left shows the system in equilibrium. The external forces are the support force $T_1$ at A, the elastic string forces $T$ at A and C, and the total weight $4W$ of the system which acts at the center of mass of the system.

We consider a virtual displacement of the system where point A stays fixed while B and D move apart so that the square is distorted into a rhombus. The center of mass will rise by a virtual displacement $\delta y_{cm}$ and point C will rise by $\delta y_C$.

It is not hard to see that $\delta y_C = 2 \delta y_{cm}$.

The only external forces that do work during the virtual displacement are the weight and the elastic force at C. So, the principle of virtual work implies

$-(4W) \delta y_{cm} +T \delta y_C = 0$.

This yields $T = 2W$.